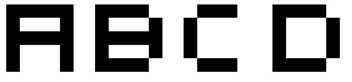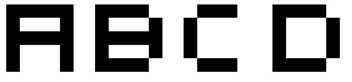The Visual System

On the necessity of a sparse code

      Let us consider (after Graham, 2005), a collection of 5 by 5 images, representing the alphabet. The first 4 letters are shown below. Over 4 millions symbols (2^25 divided by 8 (4 orientations and 2 exact inverse)) can be represented by a combination of those 25 black or white pixels. It sounds a little bit of an overkill for only 26 letters, so we could restrain ourselves to a 4*2 matrix, but it makes the picture easier. The idea is that whenever a letter is represented, the white pixels on its representation will be 'ON'. If we consider that A, B, C and D have an equal probability of occurence, each pixel is ON 56% of the time. If we had a dedicated template for each letter, it would be ON only 1/26th i.e., less than 4% of the time. From an energetic perspective, the later representation sounds more appealing. Indeed, a low firing rate seems to agree with the neuronal metabolism.

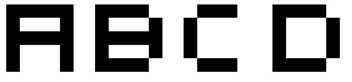
Figure 1:  A, B, C and D represented by 5*5 arrays.

Field and Olshausen's experiment

      When modelling a neural network, training stands for development and/or evolution. In the model Field and Olshausen proposed (Olshausen, 1996), the learning algorithm aimed at maximizing sparseness of the code used to represent natural images, while still accurately representing them. In short, the cost function to minimize had a first term accounting for the accuracy of the representation (mean square error between the original and the reconstruction) and a second term measuring sparsity (a non linear function of the coefficients of the representation telling how the energy is spread among the basis vectors). The first term assumes that the brain aims at giving us as much information as it can, the second term assumes that it is energy-limited.
They found a family of localized, oriented, bandpass components, which look very much like wavelets.

Figure 2:  Principal components calculated on 8*8 image patches extracted from natural scenes (From Olshausen, 1996).

Natural scenes

      Is it a surprising result? By itself maybe not: we know that natural images are sparse in a DCT or a wavelet basis for example. This is what allows compression. For the natural scene below (original on the left), if we take its DCT transform and throw away 88% of the coefficients (the smallest ones), we can reconstruct the image almost perfectly (reconstructed image on the right). More fundamentally, the concept of a best basis has been introduced (Mallat, 1999), which could provide more insight, but it was beyond the scope of this project.

Figure 3:  Example of a naturel scene before (left) and after (right) transformation. 88% of the coefficients of the DCT have been discarded.

Receptive Fields

      What was exciting about Olshausen's results though was the fact that such a basis of oriented, localized and bandpass components look very much like the set of receptive fields cells that are found at several levels in the retina and in the visual cortex.

      In the retina, the receptive field of a given bipolar cell is the circumscribed area of the retina this cell is getting input from. The photoreceptors absorb light and signal this information through the release of the neurotransmitter glutamate to bipolar cells, which in turn transfer information to ganglion cells. Bipolar cells have receptive fields with center-surround inhibition. The center is produced through direct innervation of the photoreceptors above it, either through metabotropic (ON) or ionotropic (OFF) receptors. The surround requires some processing. It probably happens through the horizontal cells. Those have synapses on both, cones in the center of some bipolar cell's receptive field and cones in the surround of some other bipolar cell's receptive field. The exact mechanism involved is not yet known (Kandell, 2001).

      Receptive fields of cells in the visual cortex can be classified into simple or complex cells depending on the stimulus triggering them (Hubel, 1959; Hubel, 1968). Orientation (stimulus in some specific orientation) and/or direction (stimulus moving in some specific direction) selectivities are important properties of those receptive fields. Therefore, the definition of the receptive field of a cell needs to be extended: it is no more the region of space where the presence of a stimulus will trigger the cell (which for bipolar cells corresponds to the area on the retina the cell is getting input from), but this region plus an orientation.

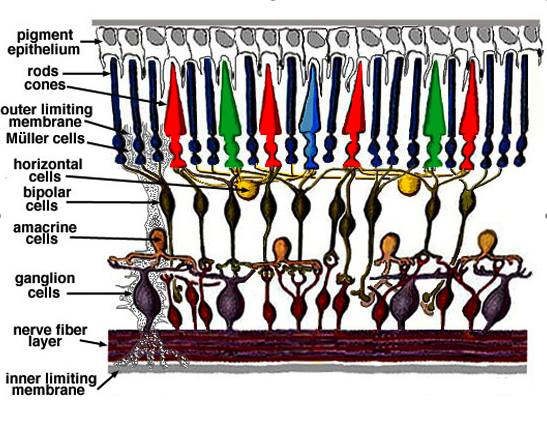
Figure 4:  Organization of the retina (From http://webvision.med.utah.edu/sretina.html). Light enters at the bottom.

Random dot kitten

      It is very tempting to conclude that the brain through development and/or evolution has shaped the receptive fields cells in order to provide us with an accurate and energy-efficient representation of the world we live in. However, one could also argue that it works the other way: since we have receptive fields cells, the world being what it is, we get a sparse representation of it. Pettigrew (Pettigrew, 1973) showed that kitten reared in the dark and exposed to a planetarium-like environment deprived of lines and edges developped receptive-field cells sensitive to spots of lights and not to edges as a kitten reared in a normal environment would do. This experiment strengthens our very tempting conclusion above.

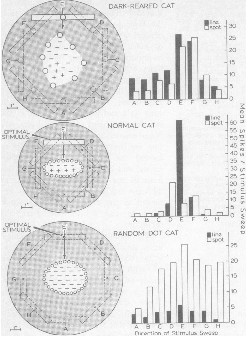
Figure 5:  Comparison of typical neurons from the striate cortex of cats raised under three conditions: (i) total absence of visual stimulation, (ii) normal visual experience, (iii) visual experience confined to randomly arranged light spots (From Pettigrew, 73).