Limitations in the Algorithm

In addition to the undesirable “echo” effect we discussed earlier, our algorithm introduces other limitations, some of which can be fixed, but others are just inevitable.  These limitations are geometrical distortion and artifacts.  

Geometrical Distortion

The formula for calculating the stereo separation is an estimation.  This approximation is what causes a slight effect called geometrical distortion.  Examine the previous two figures carefully.  In our code, let “a” be the point that represents the x value that has been reached (the horizontal point, i.e. the points that we scan across for each y).  The formula uses the distance aA to calculate the stereoseparation.   However, this is just an estimation, since the stereo separation should be dependent on the point A’ instead.  Luckily, at normal viewing distance, geometrical distortion is only a small, if at all noticeable problem.  At far viewing distances, A and A' coincides and geometrical distortion disapears.  There is also vertical distortion, similar to horizontal distortion, but again this distortion is usually unnoticeable.

Some algorithms interpolate the z-values linearly into the space between the near and far planes.  This creates a small depth distortion, since stereo separation is not a linear function of z.  The depth planes are not spaced the same distance apart, and our program correctly estimates this by using a non-linear separation function:

function r = separation(z)
DPI = 72;
E = 2.5*DPI;
mju = 1/3;
r = round((1-mju*z)*E/(2-mju*z));

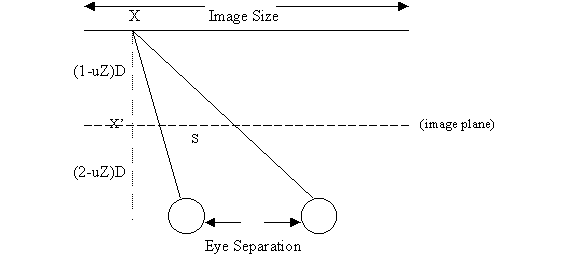
In order to keep the geometrical distortion to a minimum, we modified the algorithm to calculate the separation distance for a viewing distance of 12 inches and a image size of 5 inches.  By using similar triangles and geometrical properties, we are able to break up the viewing plane into two locations:  points that lie left/right of the eyes and points that lie between the eyes.  The figure below illustrates a point x would usually be determined to have a separation distance by dropping a perpendicular to the image plane (x').

This separation value will not be exact for extremely large images; therefore, we arrive at a more exact derivation for the separation distance where the "-/+" sign depends upon whether the location is to the left or right of the eyes, respectively.  

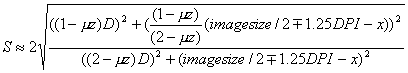
The derivation assumes the eyes are located exactly in the middle of the image and they are separated by 2.5 inches.

Artifacts

There may be an occurrence that two points, although not constrained to be the same, do occur to have the same color by chance.  This visual artifact may distract the eye when viewing the image. If we take a look at the part of the code that assigns the random colors:

for x = fliplr(1:MaxX)
  if (Same(x) == x)
   pix(x) = (rand(1)>0.5);
  else
   pix(x) = pix(Same(x));
  end;
im(y,x) = pix(x);
end;

One possible solution is to use several levels of gray instead of just black and white to reduce the probability of producing an artifact. .