Stereograms Using Bitmap Patterns Instead of Random Dots

To make the stereogram much more appealing and easier to view, we can slightly modify our algorithm for random dot stereogram to replace the random dots by bitmap patterns.  The basic idea is rather simple.  Our goal is to replace the random dots we inserted in each line with pixels from the pattern of choice.  How do we do this?  Before any constraints are added, for each line we overlay repeating blocks of the pattern we wish to insert:  repeating because we assume the width (the length of the “x-coordinate”) be smaller than the width of Z (the depth map of the object).  Then, as in the case of random dot stereograms, we scan each line and impose the necessary constraints and have the constraints override the existing pixel of pattern at that point.  For points that are unconstrained, we leave that point (which already has the pixel of the pattern in place) untouched.  The following technicalities will further clear up this idea.

  To copy repeats of the patterns in a single horizontal line, we first declare an array called pix with dimensions 1 x MaxX x dep, where MaxX is the width of Z, and dep is the third dimension of the pattern.  Starting from the very right hand side of the pix array, we place a block of pattern.  We do this by having a left pointer and right pointer to bound the width we wish to fill with the pattern.  This is done by the following lines:

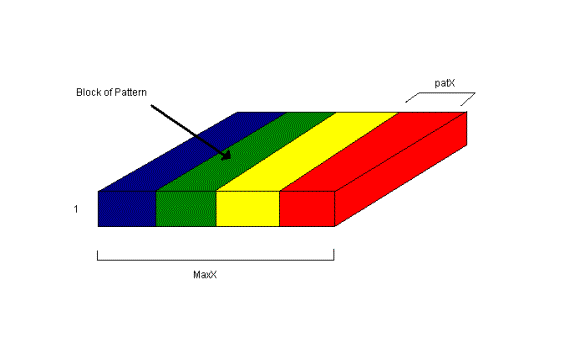
pix = zeros(1,MaxX,dep);

% copy pattern into right most portion of pix array

rightX = MaxX;
leftX = MaxX-patX+1;
pat_line = mod((y-1),patY)+1; % the vertical line of pattern to use.

% copy pattern into right side of pix array

pix(1,leftX:rightX,:) = pattern(pat_line,:,:);

We then shift the pointers, but assigning the right pointer to the pointer that was initially assigned left, and we assign the left pointer at a distance patX from the right pointer.  We again fill the space between the left pointer and right pointer with the pattern.  We repeat this process until we filled the whole pix array with repeating blocks of pattern.  Note that we have to have a condition that checks when we have filled up the whole array.  The end result of the pix array will look something like this:

There is still one minor detail that has to be discussed when placing the blocks of pattern together.  When we place the blocks together, it is not desirable to have rapid changes at the boundary, since this will cause small but noticeable patches in our resulting image.  To make a smoother transition at the boundary, instead of stacking together the same block of pattern, we stack together a block and its reversed or flipped block.  Thus, this ensures the pixel at the boundary would have the same color.  The following code performs the pattern placing as mentioned:

 
% copy a reversed line of the pattern into rest of image, reverse to avoid accidental alignment
% do this to avoid black patches

rev_pat = pattern(pat_line,linspace(patX,1,patX),:);
done = 0;
rightX = leftX-1;
leftX = rightX-patX+1;
while ~done
  pix(1,leftX:rightX,:) = rev_pat(1,patX-(rightX-leftX):patX,:);
  rightX = leftX-1;
  leftX = rightX-patX+1;
  if rightX<1
     done = 1;
  else
      if leftX<1
        leftX = 1;
      end;

  end;

end;

 

All we are left with then is to identify the constraints, then override the existing pixel with that constraint.  If the points are not constrained, leave them alone with the pattern pixel already in place.  This section of the code is almost the same as in the random dot case, with minor modifications in assigning the pixels (note in the below code the line % pix(1,x,: ) = (rand(1)>0.5) has been commented out to show that this line would of existed if we were filling up the space with random dots – we leave this line out because we already filled the unconstrained points with pixels form the pattern):

 
for x = fliplr(1:MaxX)
  if (Same(x) == x)
     % pix(1,x,:) = (rand(1)>0.5);
  else
     pix(1,x,:) = pix(1,Same(x),:);
  end;
  im(y,x,:) = pix(1,x,:);
end;