Say What, Einstein?

In programming terms

The depth map Z is a function of both x and y.  The screen is set maxX by maxY pixels.  We have a large outer for loop that scans one horizontal line at a time.  Inside this big loop, on the first pass, we set the appropriate pixel value for each corresponding pair of points (associated with each point on the depth map).  This will constitute another “for” loop inside that scans from left to right.  In the second pass, we scan in the reverse direction, from right to left, and set random values for points that are not already constrained.  This constitutes a second “for” loop within the big “for” loop.

In the first inner loop, we first calculate the stereo separation associated with each point of the depth map along x.  Next, we find where the two points lie according to their separation, and denote these points “left” and “right”:

leftpointer = x – round(s/2);

rightpointer = leftpointer + s;

The next part of the code deals with the concept of “hidden surface removal”, and we will skip this part of the discussion for now.

To ensure that the pixel at “left” is the same as that of “right”, we have the line:

SamePix(leftpointer) = rightpointer;

Now, we have to be aware of the possibility that the  “left” value is already constrained as we scan from left to right.    This occurs when the "left" point coincides with the "right" point of a previous assignment.  If the "left" point does coincide, we move the pointer until we find an unconstrained point.  The following couple of lines will do the job:

 while ((l ~= leftpointer) & (l~= rightpointer))
  if (l<rightpointer)
  leftpointer = l;
  l = SamePix(leftpointer);
 else
  SamePix(leftpointer) = rightpointer;
  leftpointer = rightpointer;
  l = SamePix(leftpointer);
  rightpointer = l;
 end;
end;

All constraints are set for all pixels when we finish scanning left to right.  The next step is to scan backwards and find which pixels have not be assigned, and then randomly give values to them.  We do not alter the pixels that have been assigned:

 
for x = fliplr(1:MaxX)
  if (Same(x) == x)
   pix(x) = (rand(1)>0.5);
  else
   pix(x) = pix(Same(x));
  end;
im(y,x) = pix(x);
end;

Now we revert back to our discussion on “hidden surface removal”.  Examine the following figure. 

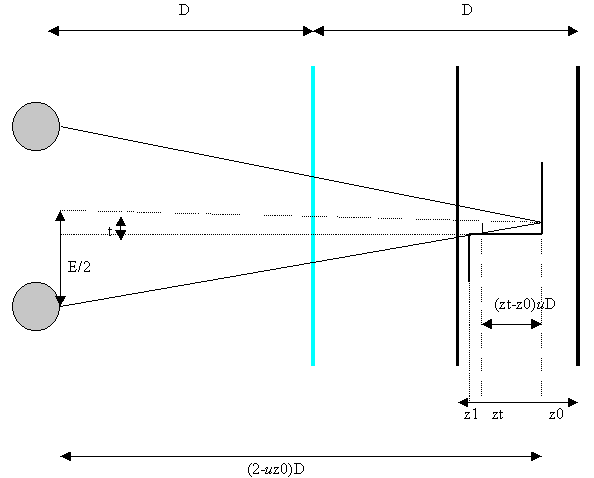
We see that it may be the case that part of the object in the near plane may obstruct the eyes’ view of a point in the far plane.  For any part of the object that is obstructed or “hidden” from our view, we can remove that point.  This gives greater flexibility in assigning pixel values, and reduces a problem called “echoes” in our image. 

What are echoes?

As mentioned previously, there may be a coincidence that three points in the plane are equal to each other.  The outer points are equal to each other, even though it is not meant to be the same.  The fact that these outer points are equal creates an artificial point in the image.  This phenomenon is what is known as echoes.  Echoes are undesirable because they cause distortions in the image.

Hidden surface removal reduces the problem of echoes, by reducing the constraints such that echoes in the same plane as the figure are minimized.  To implement hidden surface removal, we note from the figure that the criteria for hidden surface removal is that z₁ >= z_t.  A point is not visible to the eye when t is greater than 0 and up to the condition that z_t=1.  Using similar triangles of the small shaded triangle with the large one, we get:

 t/[(z_t-z₀)uD] = E/[2D(2-uz₀)]

 rearranging, we get

z =z₀ + 2(2-uz₀)t/uE

 The piece of code that performs the hidden face removal is given below:

t = 1;

visible = 1; zt = 0;
while (visible & ( zt < 1 ))
   zt = Z(y,x) + 2*(2 - mju*Z(y,x))*t/(mju*E);
   visible = (Z(y,x-t)< zt) & (Z(y,x+t) < zt); 
 t = t+1;

end;

The inequality z1>=zt and the test for whether the eye’s view is being obscured, is given by

visible = (Z(y,x-t)< zt) & (Z(y,x+t) < zt);

This operation is done for the range of t (the range where the point is not visible).