
More Technicalities …
Before
diving into the algorithm used to generate random dot stereograms, we

Imagine looking through a transparent glass, with an object placed behind the
glass, as shown in the above figure. When
we look at a particular point on the object, two rays can be drawn from that
point, one to each eye. The rays to
the left and right eyes pass through different places on the screen.
For parts of the object that are close to the screen, the separation will
be smaller than for more distant points. If
both rays are the same color and intensity, they can be conveniently reproduced
by a single light source in the image plane.
This fact explains how a stereoscopic picture can be viewed without any
special equipment. One image in the image plane, not two, can be shared by both
eyes even though the object can be seen stereoscopically.
The
above figure also shows that if we chose two locations of the solid object just
right, they can generate 3 dots or images on the plane, with two of them
coinciding. Since the central dot
represents two different locations on the object, and if the central dot is of
one color, this implies that the other two dots on the image plane must have the
same color. By using similar
triangles, we can calculate the stereo separation as:
Stereo
Separation = (eyesep*depth)/(depth+observer_dist)
Two similarly colored points placed on the screen with this separation can represent a virtual point behind the screen. If we diverge our eyes as if looking through the screen, we can reveal a 3D image, and thus able to generate an “autostereogram”.
The above equation for calculating stereo separation is general and needs refinement. Specifically, we need to find what ‘depth’ in the calculation represents. Consider the figure below:
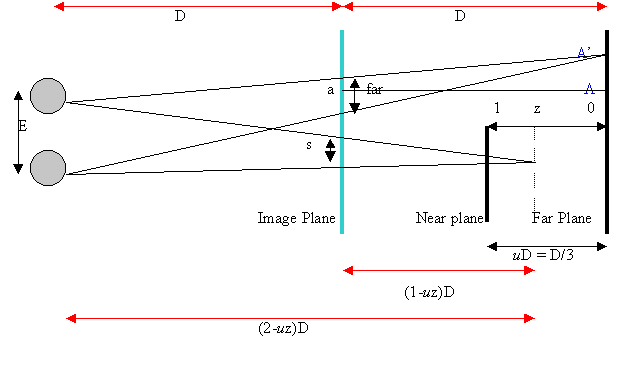
The
object lies between the planes labeled ‘near’ and ‘far’.
We chose the far plane to have a distance D from the image plane, which
is the distance from the image plane to the observer.
This choice aids in the ability to view the autostereogram when it is
produced, since if we look at the reflection in the screen our eyes will
converge on the far plan, assisting in the convergence process necessary to view
the stereograms. The near plane is uD in front of the
far plane, in which we have chosen u=1/3
for our program. We have chosen u=1/3
since it isn’t so large that it will cause difficulty in attaining proper
convergence of the eyes. The
parameter u is crucial because the separation between the near and far plane
determines the depth of field. If
the depth of field is too large, it will be hard for our eyes to converge, and
thus harder to view the image. From
the figure, we can use similar triangles to obtain a more informative expression
for the separation distance s:
S=
(1 –uz)E /(2-uz)
Now
that we are armed with this knowledge, we are ready to begin the discussion on
how autostereograms are implemented.