Results

Image Rotation: The Shape Phantom

The methods do not perform equally in the presence of rotation. In the data shown below, unshifted phantoms (tx=ty=0) were rotated over a range of small angles and the results of the rigid body and affine registrations were compared in the same manner as the previous figure. First, we'll consider the results from the shapes phantom, shown in the figure below.

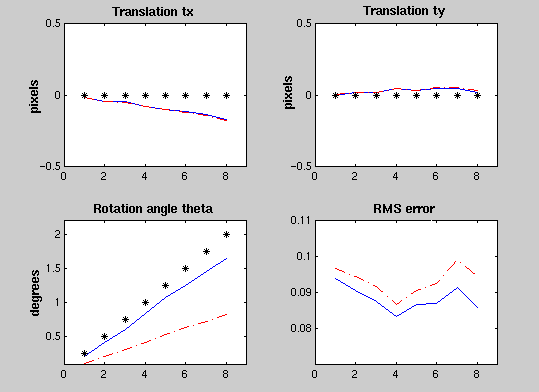
Algorithm performance on small rotations applied to the shape phantom (theta<=2 degrees). The format is the same as the previous figure. The theta shown for the affine registration is estimated from Sx and Sy. Note that the error is consistently higher for the affine registration.

Interestingly, the affine registration scheme consistently has higher error than the rigid-body scheme, despte the extra degrees of freedom in the affine model and small-angle approximation implicit in the rigid-body method. An intuitive measure of the goodness-of-fit of the two methods is to apply the found rigid-body and affine transformations to the image that has undergone motion. We can then compute the difference between this corrected image and the original image that it is has been registered to. The difference images for a 2 degree rotation are shown below for the two algorithms (along with the original images for comparison).

Unrotated image (Im0)	Rotated 2 degrees (Im1)
Rigid body transformation (Im0-Mr*Im1)	Affine transformation (Im0-Ma*Im1)

The rigid-body transformation does a good job correcting for the rotation, showing essentially no features of the shapes phantom in the difference image. The affine transformation clearly has not corrected for the rotation, as the difference image shows prominent features of the rotation.

More results

Index