Results

Image Rotation: The Shepp-Logan Phantom

When the same set of rotations are applied to the Shepp-Logan phantom, neither algorithm is able to estimate the rotation, as shown below. Once again, despite the extra parameters available in the affine method, the rigid-body registration has lower RMS error.

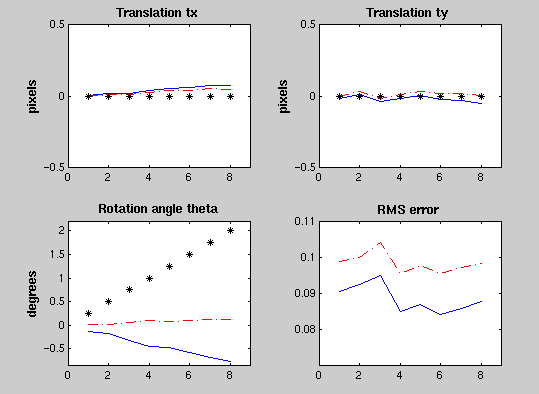
Algorithm performance on small rotations applied to the Shepp-Logan phantom (theta<=2 degrees). The format is the same as previous figures. Note that, although neither method is correctly estimates the rotation angle, the error is again consistently higher for the affine registration.

Upon inspecting the Shepp-Logan phantom, it is probably not surprising that neither method performs well. Due to the fairly circular nature of the phantom and dominantly low frequency content of the image, rotations about the center of the image are difficult to detect, even for the human observer. This is perhaps worrisome, given that the Shepp-Logan phantom is meant to mimic the human brain. However, the sulci and gyri found in the brain may provide sufficient high frequency information to improve the performance on a real subject. The rotated images are shown below, along with the difference images in the same format as for the shape phantom.

Unrotated (Im0)	Rotated 2 degrees (Im1)
Rigid body transformation (Im0-Mr*Im1)	Affine transformation (Im0-Ma*Im1)

(yes, there's...) More Results

Index