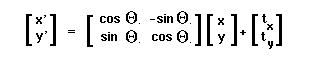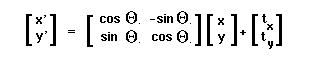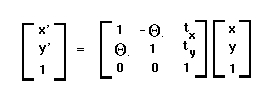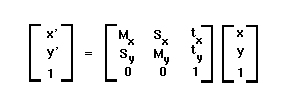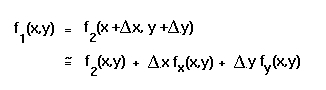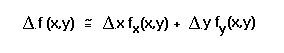Methods
Image Registration for fMRI
We want to remove the small (sub-pixel) motions that often occur
during a single fMRI scanning session with cooperative subjects. For this
particular problem, we can make 3 assumptions:
- motion conserves intensity (motion is in-plane)
- motions are affine (constrained to translation, rotation & shear)
- motions are small (a few pixels at most)
This study considers two simple motion models that can be linearized
based on the above assumptions.
Rigid Body Transformation (Rotation and Translation)
With the above assumtions, we can consider motions to be operations on
the image (pixel) coordinates. Thus, translations are described by
adding some constant amount (tx,ty) to each coordinate. Rotations are
described by a rotation angle theta. A motion that is comprised of a
rotation followed by a translation can be described by the operation:
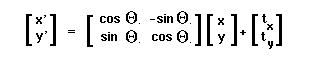
Since motions are assumed to be small, we can use a small angle
approximation for the rotation (expressed in homogenous coordinates):
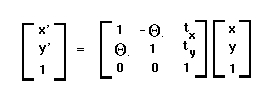
Note that, by making the small-angle approximation, we have found a
set of equations that are linear in our parameters tx, ty and theta.
The Affine Transformation
The affine transformation allows for a wider range of linear
transformations than the rotation and transformation system already
presented (see Bracewell). The rotation matrix is replaced by four parameters: Sx and
Sy represent shear operations, and Mx and My represent
magnification. This transformation is linear in the absence of approximations:
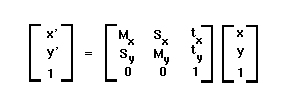
Note that, for 2D images, the affine transformation has twice the
number of parameters of simple rotation and translation (6 vs. 3).
Linearizing Motion
Because we are assuming only small displacements of the coordinates of
one image relative to the other, we can linearize the displacement
using a first-order Taylor approximation:
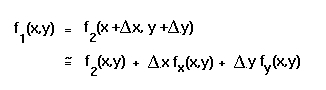
That is, we can express the displacement at a pixel in terms of the
partial derivatives of the images and the functions delta-x and
delta-y.
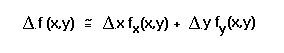
For the rigid-body and affine transformations described
above, delta-x and delta-y are linear functions of x and y.
This linearization allows us to find a least-squares optimal estimate of
the motion parameters for both the rigid-body and affine motion models
by simply computing a pseudoinverse matrix. Taylor approximations
appear to be fairly common linearizations of motion systems (Friston, Nestares).