Milton Chen Wolfgang Prymas

The Super-Resolution Algorithm

This algorithm was first described in Irani and Peleg, 1990.

Given several images of a scene, together they potentially contain more information than any single one. Detail, that is lost due to decimation (the quantization process) and blur (optical and sensor characteristics), could be recovered. In a sense, one can think of such a  resolution enhancement procedure as a process of intelligent image fusion, that recovers most of the original information.

Simply increasing the number of pixels, interpolating and averaging over multiple frames, often improves the quality and is typically used as a starting point. To go beyond that, knowledge of the imaging process and the viewing geometry is necessary. The further, to simulate the imaging process and the latter to match the various frames accordingly. If the camera or sensor geometry (viewing position, angle, distortion etc.) is known, then the geometric transformations can be directly incorporated in the imaging and reconstruction process. If the geometry is not known , i.e. multiple overlapping frames of unknown origin, then the images have to be registered. More on Image Registration here.

So how is it done ?

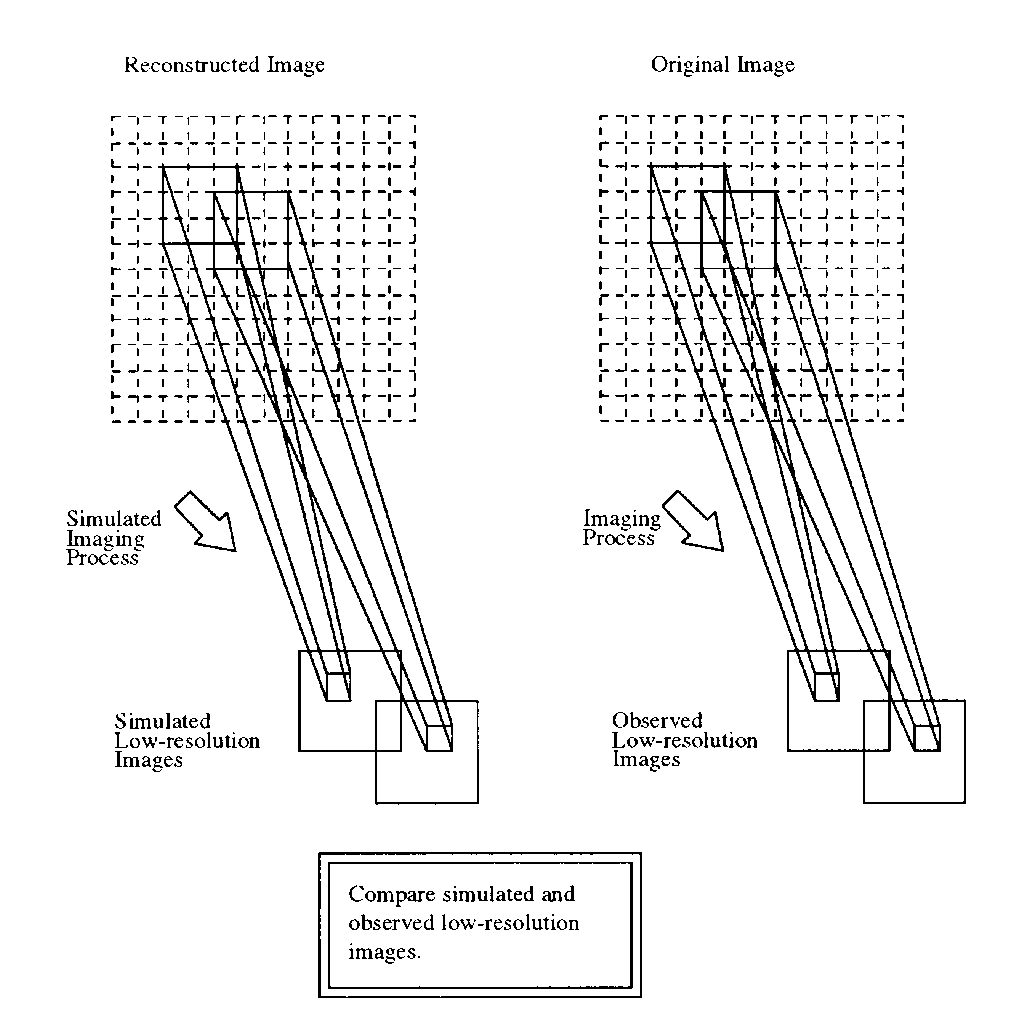
The principle idea is to simulate the image formation process, to generate a set of low resolution images that resemble the original images. The simulated images are generated from an initial high resolution image (an initial estimate, based typically on an average). By comparing the generated images with the originals one can iteratively adjust the high resolution image to successively minimize the difference between the original and simulated low resolution image.
 

Imaging Model, more precisely and in detail:

We start with a set of low resolution images {g_k}. There are k original images.

• f  is the desired high resolution image. Finding f is the objective of the super-resolution algorithm.
• T_k  is a 2-D geometric transformation, in our case an affine transformation from f to g_k. T_k is assumed to be invertible.
• h  is a blurring operator, determined by the Point-Spread-Function (PSF) of the image acquisition sensor (CCD, scanner).
• h is assumed to be Gaussian.
• s is the down sampling operator, which digitizes and decimates the image into pixels and quantizes the resulting pixel values.

The goal is now to construct a higher resolution image f', which approximates f as accurately as possible and surpasses the visual quality of the observed images in {g_k}. It is assumed that the acceleration of the camera is negligible.
 

The Iterative Process

Starting with an initial guess f⁽⁰⁾ for the high resolution image, the imaging process is simulated to obtain a set of low resolution images {g_k⁽⁰⁾} corresponding to the observed input images g_k. If f⁽⁰⁾ were the correct high resolution image, then the simulated images {g_k} should be identical to the observed images. The difference images (g_k - g_k⁽ⁿ⁾) are used to improve the initial guess by "back projecting" each value in the difference images onto its receptive field in f⁽⁰⁾, yielding an improved high resolution image f⁽¹⁾. This process is repeated iteratively to minimize the remaining error.
 

This iterative update scheme of the high resolution image can be expressed by:

Deblurring

Without up- and down sampling the algorithm has the effect of deblurring:
In this case the imaging process is expressed by:

Choosing h and p:

An important part of the algorithm is the selection of the blurring operator h. The amount of blurring should approximate the actual properties of the imaging sensor (Point-Spread-Function).

Even more critical is the right choice of the backprojection operator p.

The diagram below explains the simulation process: Multiple pixels in the high resolution image (those in the region of support of the blurring operator) contribute to a single low resolution pixel. Since these areas overlap, it is also the case that multiple pixels in the low resolution image are influenced by the same high resolution pixel (some stronly and others weakly). The backprojection operator collects these contributions in a convolution operation  and when applied iteratively has a de-blurring effect.   
 

Related work

Above described method can also be applied to color images, for example to multiple frames of a Video sequence. Due to the specific color perception of the human visual system, it is usually sufficient to apply the enhancement to the Y-component (luminance) and use simple averaging for the chrominance components.

Cheeseman et al have developed a statistical method, namely a form of Bayesian estimation, assuming pixel neighbor correlation, to improve on the Super Resolution algorithm. The Bayesian approach shows dramatic resolution enhancement for images of the Martian surface gathered by the Viking Orbiter.
 

(up) (prev-page) (next-page)