Critical Flicker Fusion Distance

PSYCH 221 Final Project

By Sheila Bijoor (sbijoor) and Daniel Golden (dgolden1)


Introduction and Motivation

The human visual system interprets information from visible light in the environment by periodically sampling images projected onto the retina. The sampled information is then integrated by the visual system to form complex decisions about whether an image is stable or moving. In some cases, however, the periodicity in which the eye samples leads to limitations in its responsiveness to change. When intermittent stimuli are presented, the visual system's perception of whether the stimuli are separate, flickering, or "fused" (i.e., multiple stimuli appearing as a single static stimulus) depends on multiple factors. These factors include (1) luminance, or brightness, of the stimuli (Hart Jr, WM 1987), (2) chromaticity, or color irrespective of brightness, of the stimuli (Kelly 1974), (3) frequency at which the stimuli are alternated (Truss 1955), (4) the retinal position of stimuli, or whether it excites rods or cones (Tyler and Hamer 1990), (5) size of stimuli (Hecht and Smith 1965), and others.

In this project, we investigate the effect of color contrast on the eye's ability to identify flickering images. We wish to determine:

(1) the critical chromaticity and luminance distance between the a base and alternate stimuli before which alternations between the base and alternate are seen as fused. We call this distance the Critical Flicker Fusion Distance (CFFD).

(2) how the CFFD depends on the particular subject characteristic of Red-Green color-blindness.

We compare our results to previous work on this subject by Truss in 1955, in which he measured the chromatic flicker fusion frequency (CFFF) as a function of the chromaticity and luminance difference between pairs of colors presented alternately.

Experiment Methodology

Equipment

To administer our experiment, we used the Psych Toolbox (http://psychtoolbox.org), a set of third-party scripts for Matlab. The Psych Toolbox uses specially compiled code in order to interface directly to the computer's video card, while avoiding Matlab overhead. This allows for very precise timing when performing vision-related psychophysical experiments. However, because of the complexity required for this interface into the video hardware, the Psych Toolbox is initially fairly difficult to install and work with; we probably spent as much time attempting to install the bloody thing as we did working with it.

Past experiments have shown that the refresh rate of typical LCD monitors (60-85 Hz) is often at or below the human threshold for flicker fusion. LCD monitors typically have lower refresh rates than what modern video cards can support because of their slow "response times," i.e., the time it takes for a pixel to completely change from black to white and back again. Thus, we decided that LCD monitors - despite their prevalence in our office, where the tests were administered - would not be suitable for our test. Instead, we selected a lonely, neglected CRT monitor (a KDS "VisualSensations" piece) that had been sitting on the corner of Sheila's desk, collecting dust, since her matriculation into our research group. Although the monitor was somewhat dim (indicating a smaller-than-usual gamut), it did allow for refresh rates up to 120 Hz (not true for many other CRTs that we tested). 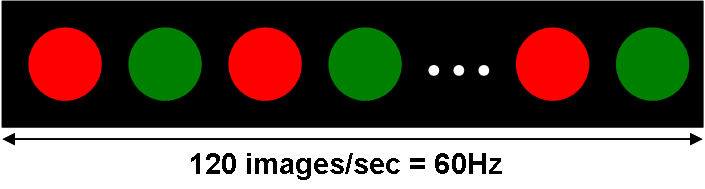Therefore, this lonely pauper of a monitor quickly became the prince of our psychophysical experiment. Note that a refresh rate of 120 Hz allows for a maximum flicker frequency of 60 Hz (see below image).


Initially, we intended for our experiment to traverse multiple flicker frequencies and Base/End color pairs. However, during our initial testing of the experiment, we determined that any flicker frequencies below 60 Hz (e.g., 30, 20, 15 Hz) were too easy to perceive, and therefore not useful for our experiment. Thus, our experiment was conducted using only the 60 Hz flicker frequency.

We calibrated the VisualSensations monitor using a PR650 spectral photometer measurement device and the Dmtoolbox Matlab code provided by the Stanford Vision, Imaging Science and Technology Activities (VISTA) laboratory at Stanford. The calibration procedure consisted of activating the monitor phosphors in different linear combinations and measuring the resulting spectral power distribution (SPD) of the display (below). This calibration data was useful in our experiment to convert from absolute color spaces, such as CIE LAB and XYZ to the proper values to input into the VisualSensations's RGB framebuffer.


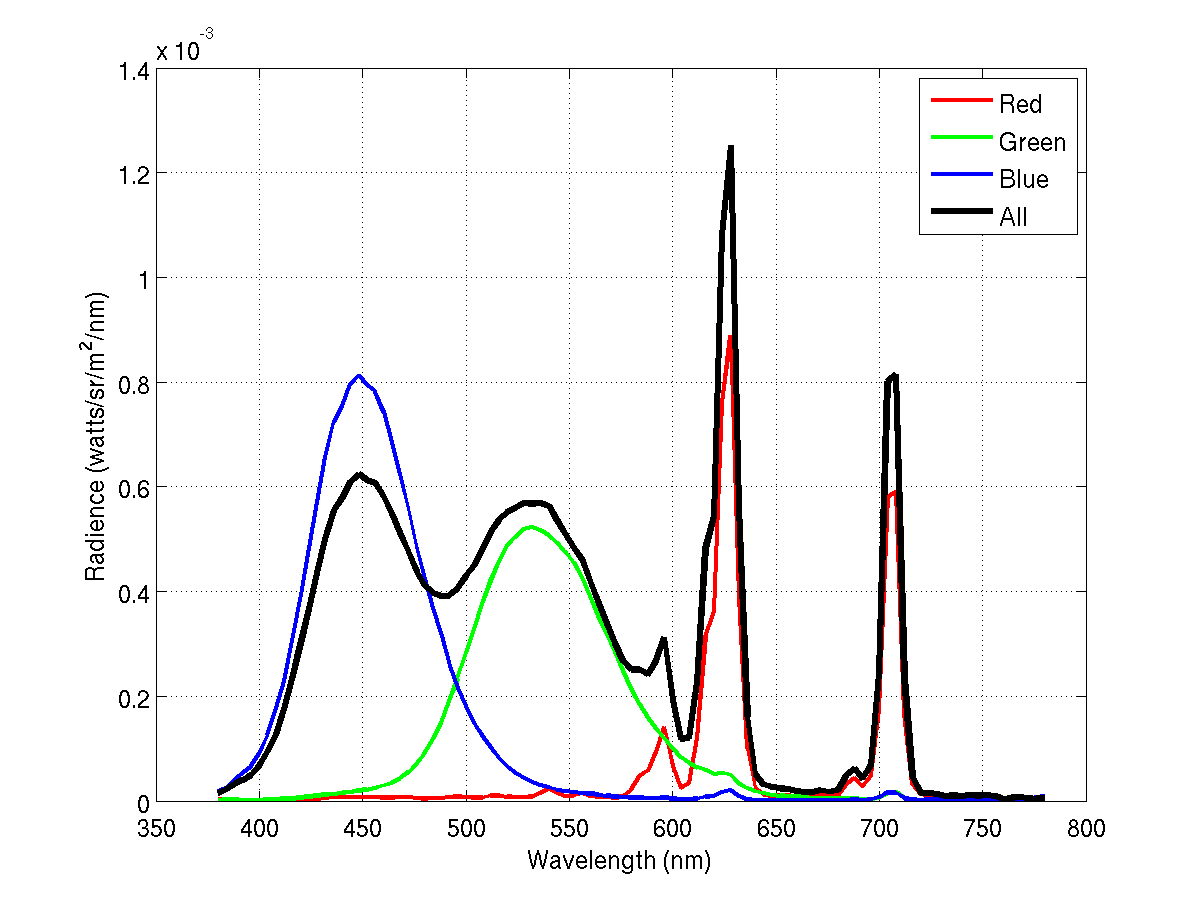SPDs from calibration of KDS VisualSensations CRT monitor.

Experimental Procedure

Our experimental procedure was a follows. The user was shown two stimuli in random order: (1) two collocated circles of color, flickering at 60 Hz, and (2) the geometric mean in CIELAB space of those two colors (it was later pointed out to us that the color that would better approximate the "mean" of the flickering colors would have been the geometric mean in RGB space -- oops). The user was then asked to select which of the two stimuli was the flickering one: either the first, or the second.

We implemented a "staircase" procedure in our threshold detection. Beginning at the "top" of the staircase (a Base/Alternate color pair for which the two colors are distant from each other, for which flickering is easy to detect), the subject may advance one step down on the staircase whenever they correctly identify the flickering pair three times in a row. One step down on the staircase corresponds to a Base/Alternate color pair that is closer together in the CIELAB Euclidean norm sense (i.e., for which flickering is more difficult to discern). If the user incorrectly identifies the flickering pair, they immediately advance one step up on the staircase, bringing them to a Base/Alternate color pair that is further apart in CIELAB space (i.e., for which flickering is easier to discern). Every time the subject switches direction on the staircase, this is known as a "reversal." The trial with any given Base/End pair ends when either the subject has undergone four reversals, or has reached the bottom of the staircase (which, in each case, corresponds to the eighth Base/Alternate pair). The full experimental procedure is summarized below.


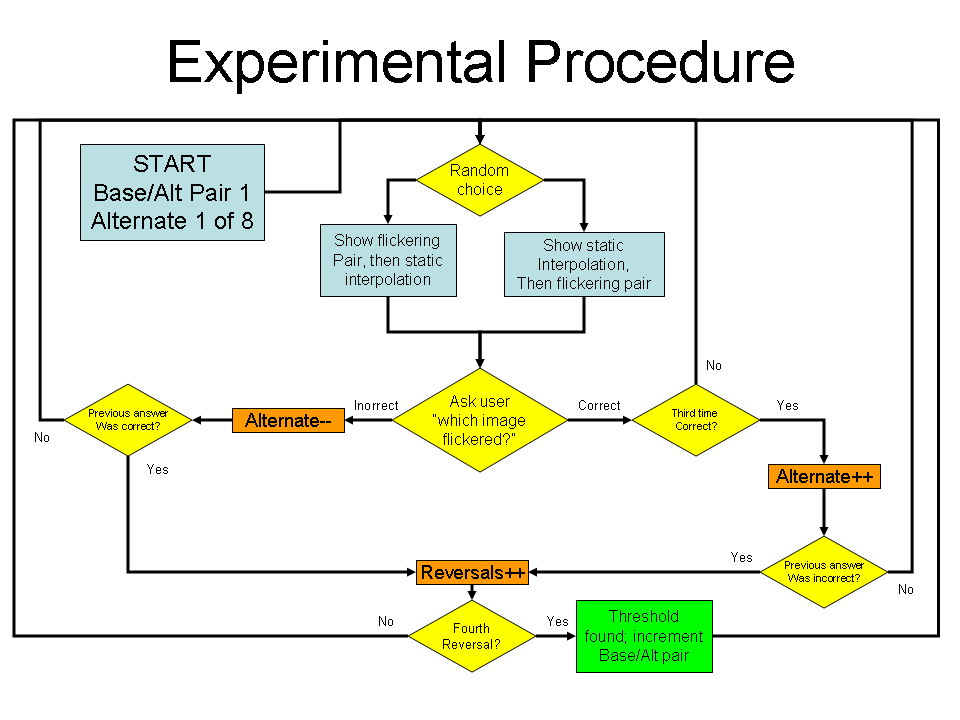Flowchart for Experimental Staircase Procedure

Color Choices

We chose six different Base/End color pairs for this experiment. A Base/End color pair consists of the "Base" color and eight "Alternate" colors. The first Alternate color is the "End" color, and there are seven linearly interpolated colors (in CIELAB space) in between the Base and End colors. The staircase begins by flickering the Base and End colors; each movement down the staircase corresponds to flickering the same Base, and the next closer Alternate color to the Base.

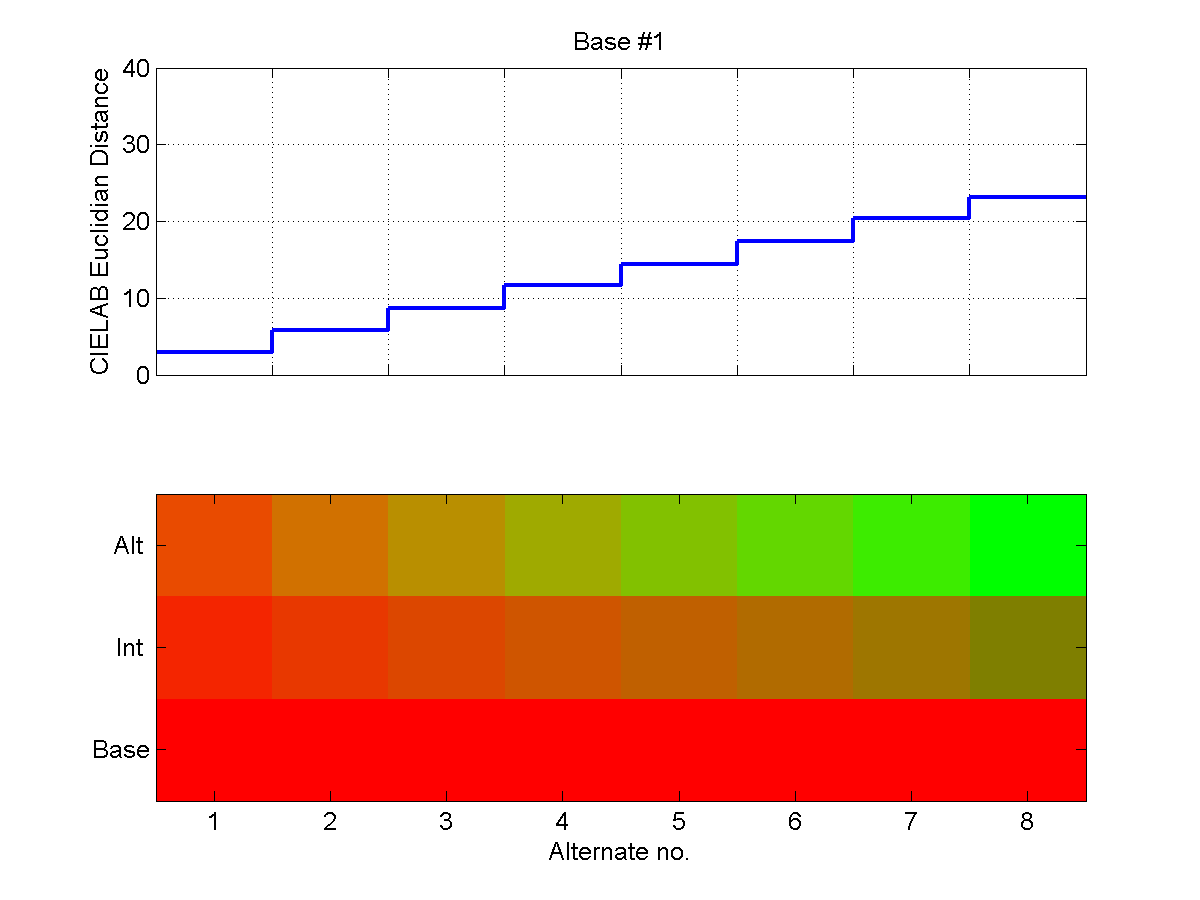
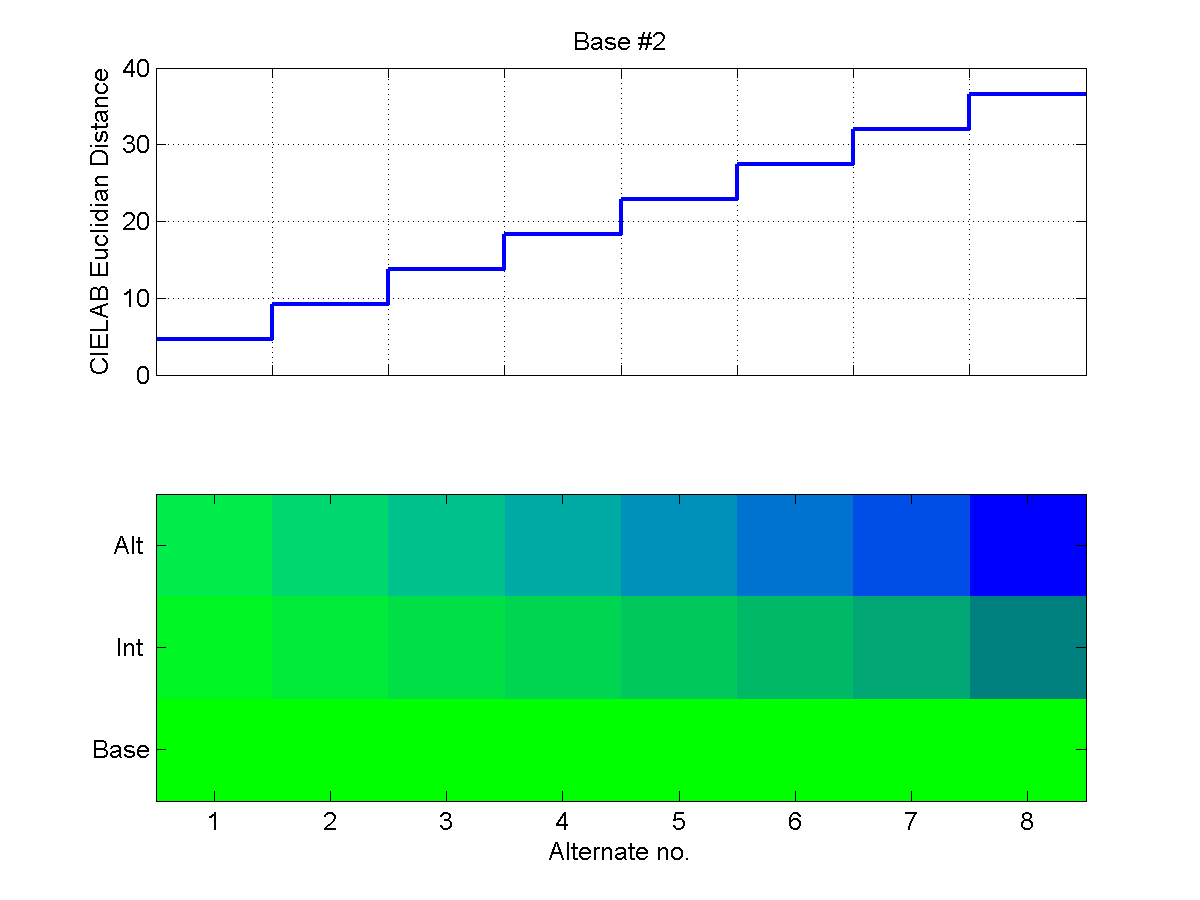
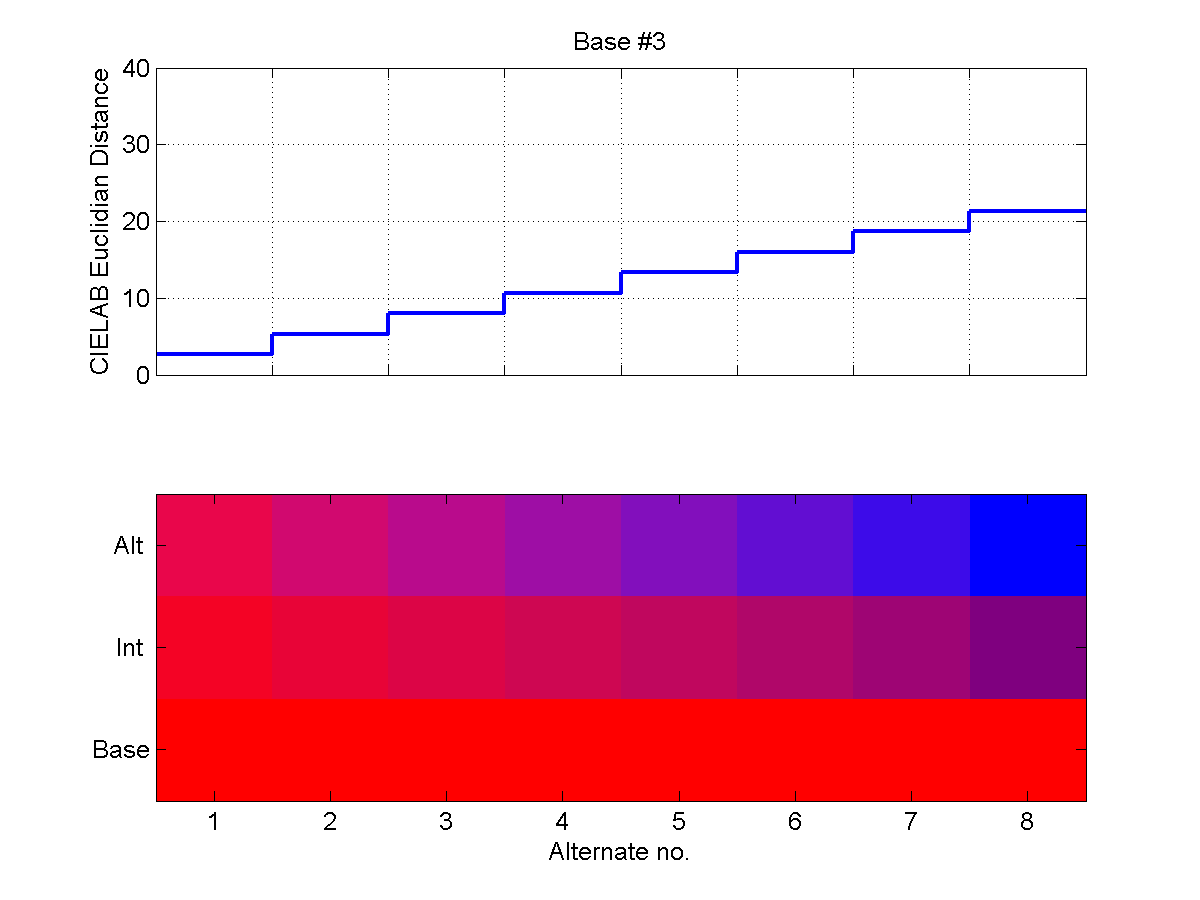
In addition to the three possible RGB Base/End color pairs, namely Red/Green, Green/Blue and Red/Blue, we also used Black/White, Purple/Yellow and Orange/Green. These Base/End pairs are summarized in the below table.

Base/End Pair
 		RGB Coordinates
 		Max CIELAB Euclidean Distance
Red/Green
 [1 0 0]/[0 1 0]
 25
Green/Blue
 [0 1 0]/[0 0 1]
 35
Red/Blue
 [1 0 0]/[0 0 1]
 20
White/Black
 [1 1 1]/[0 0 0]
 35
Purple/Yellow
 [0.5 0 1]/[1 1 0]
 40
Orange/Green
 [1 0.5 0]/[0 1 0]
 15

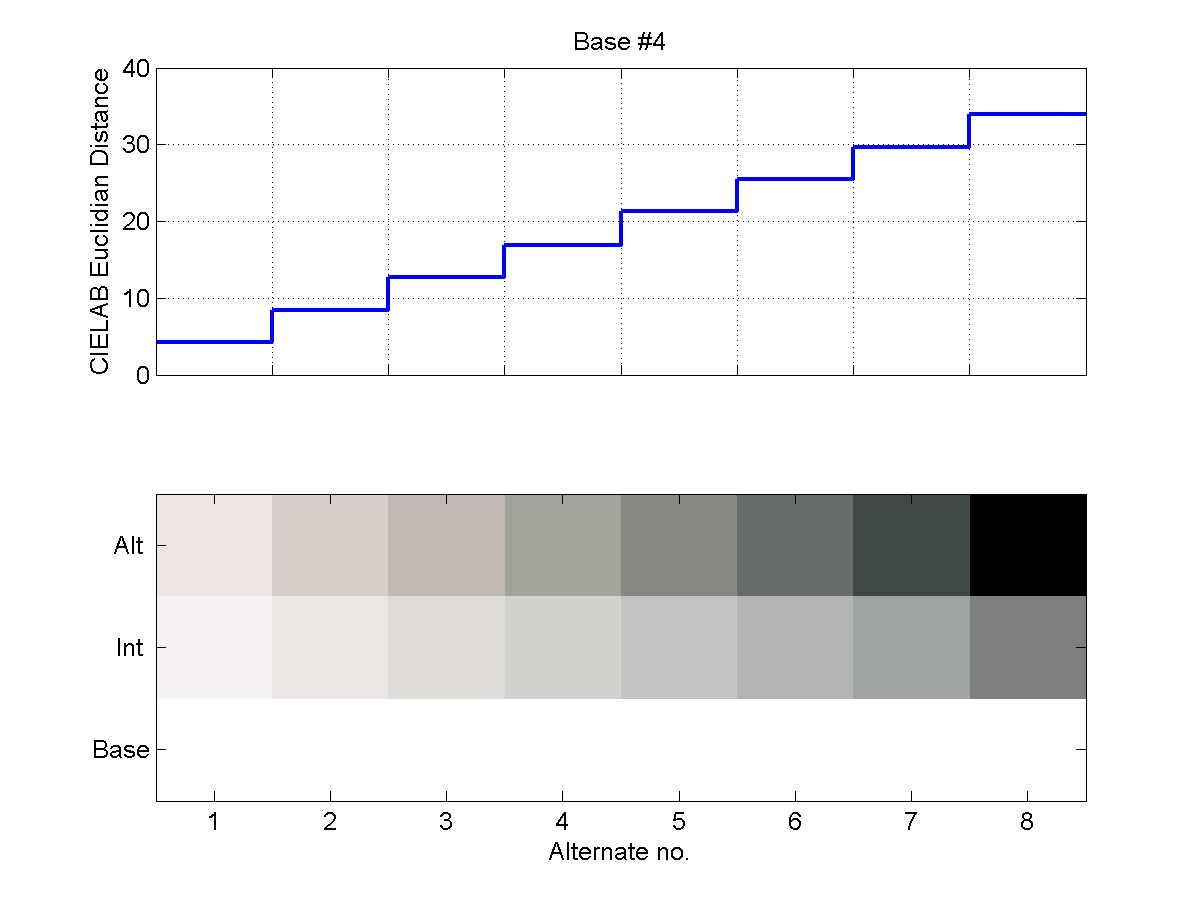
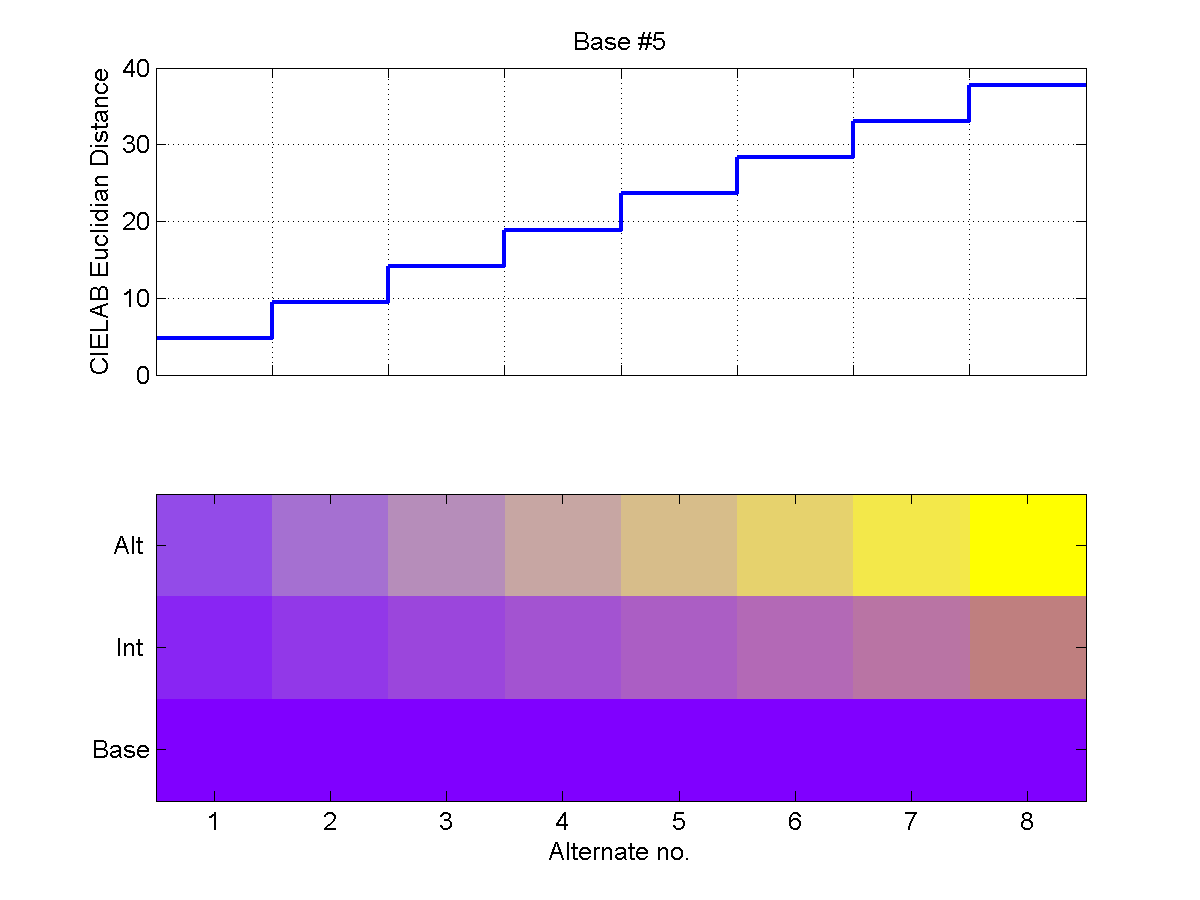
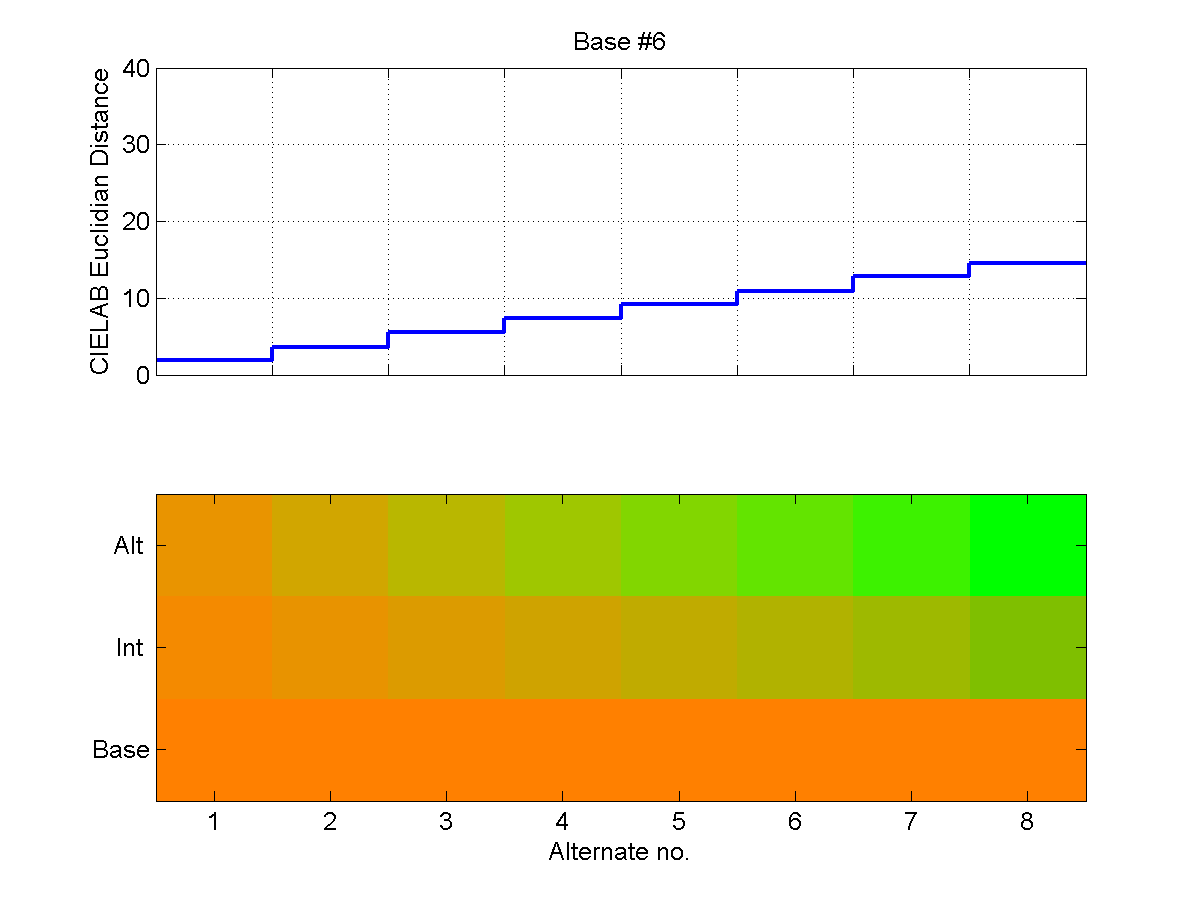
The following six two-part plots show the steps on the staircase for each Base/End pair. In the upper portion of the plots, the CIELAB Euclidean distance is shown for each Base/Alternate pair. In the lower portion of each plot, the Alternate color is shown at the top, the Base color is shown at the bottom, and the linear CIELAB interpolation is shown in the middle. Note that these plots were generated with the same RGB values that were shown on our test monitor, but because of differences in gamma and calibration, they will necessarily look somewhat different on the medium on which you happen to be viewing them than they did on our test monitor.


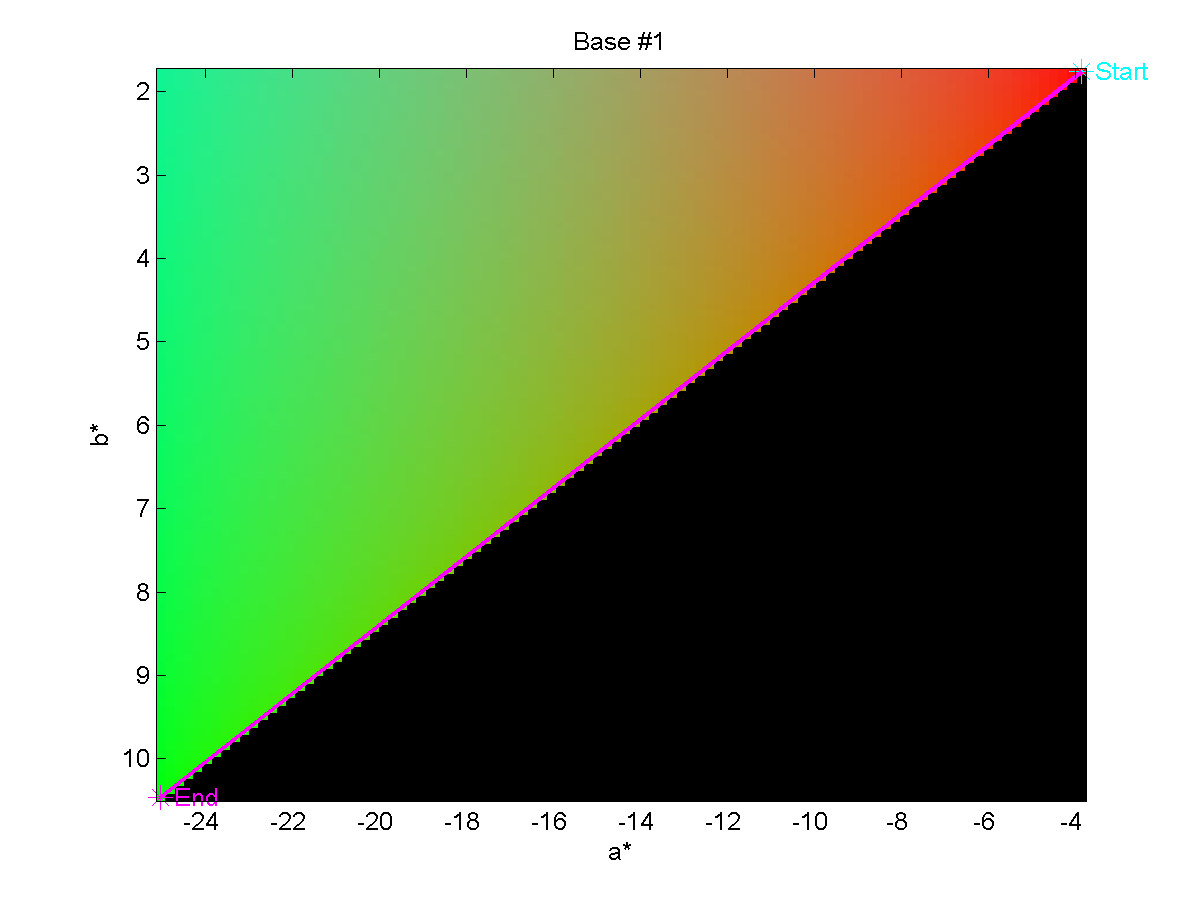
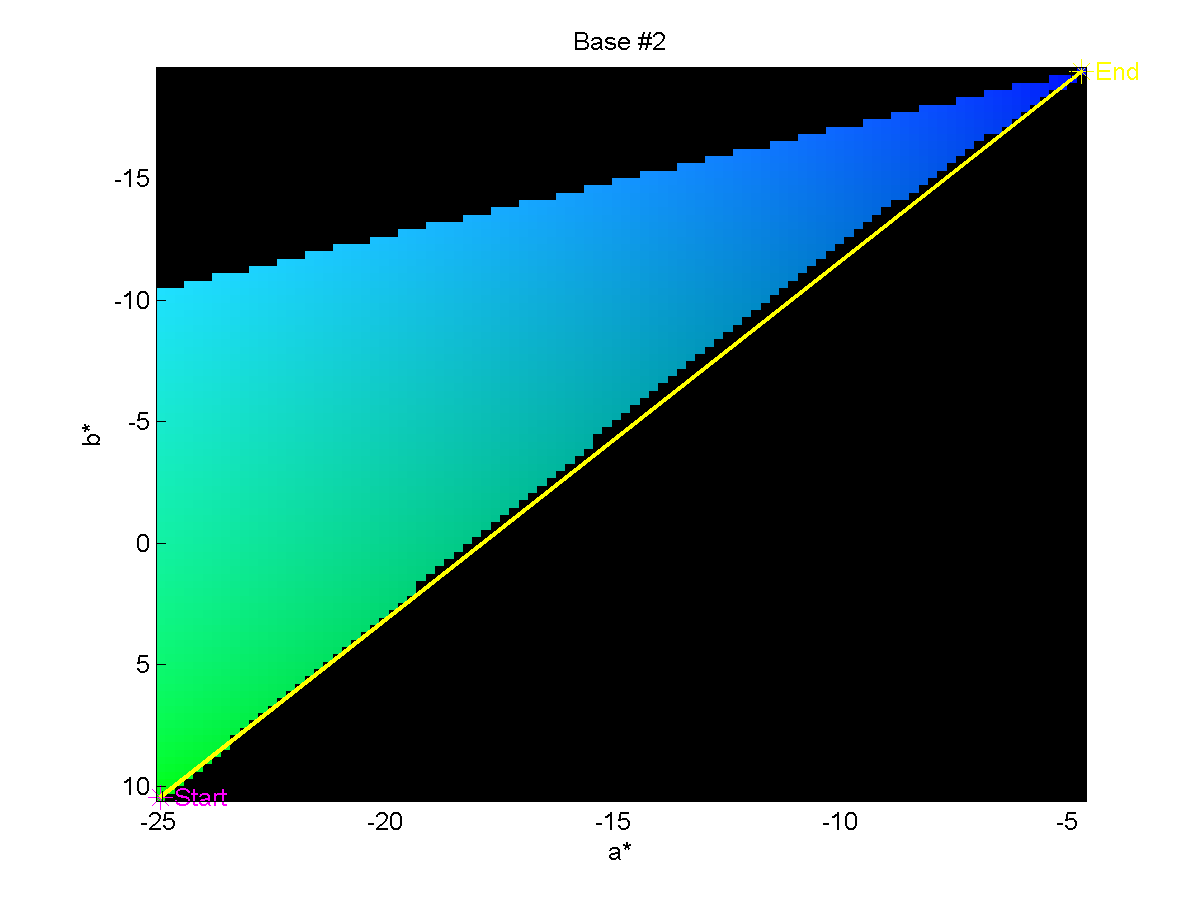
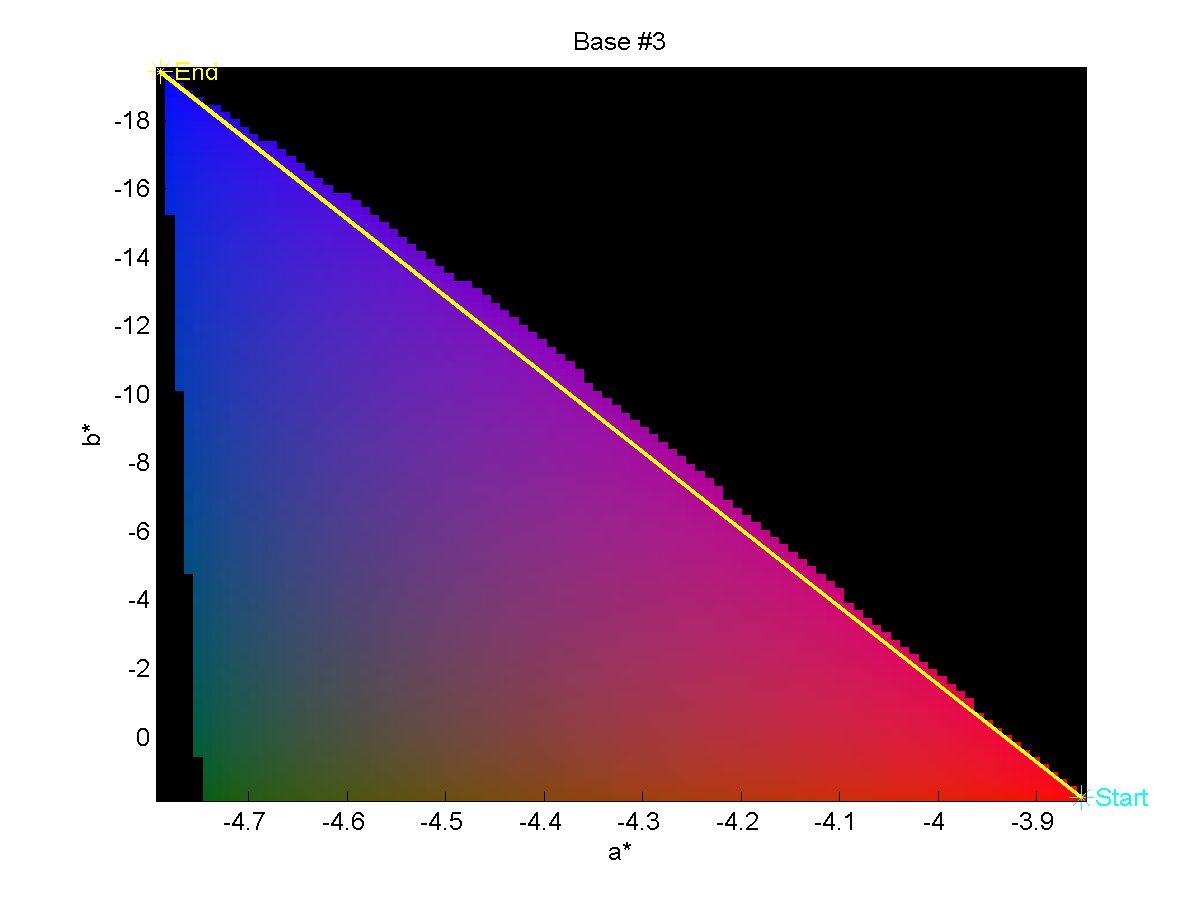
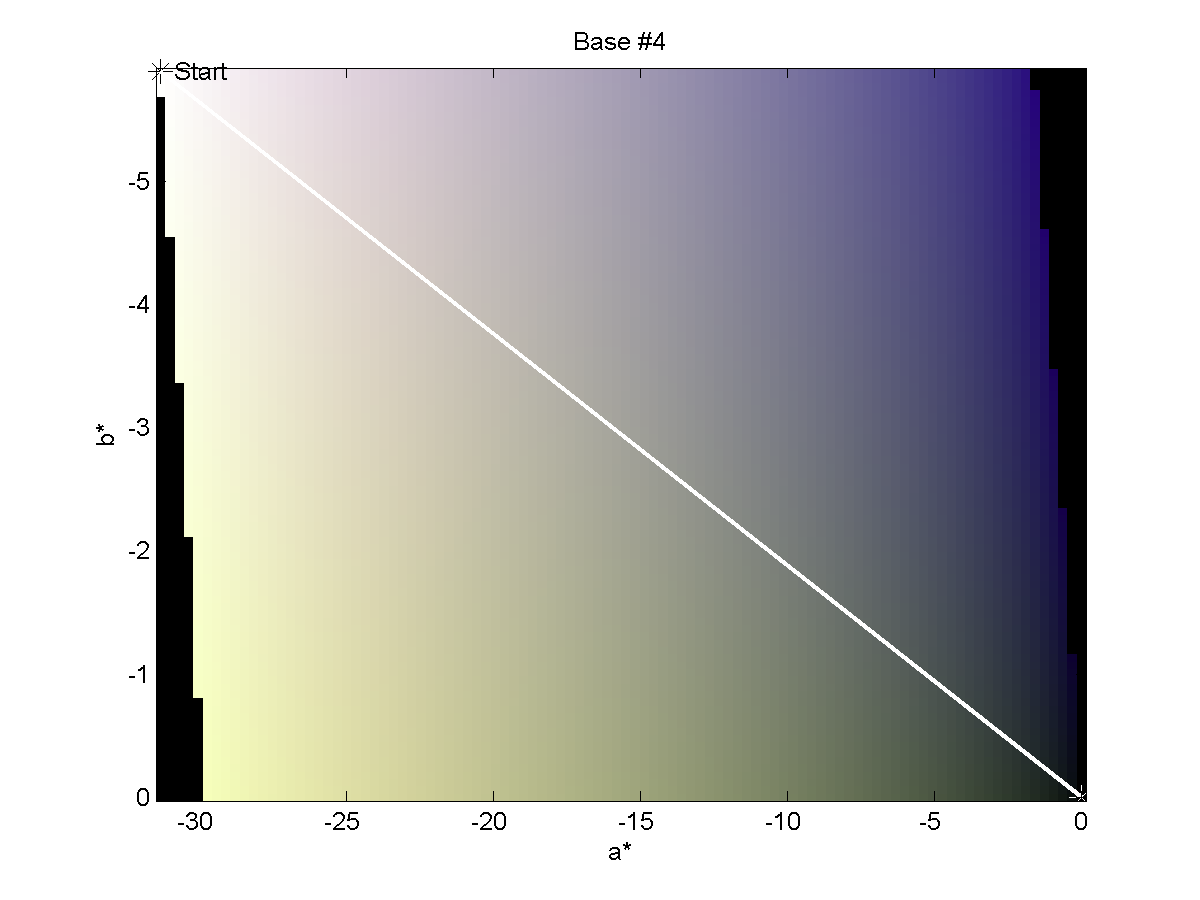
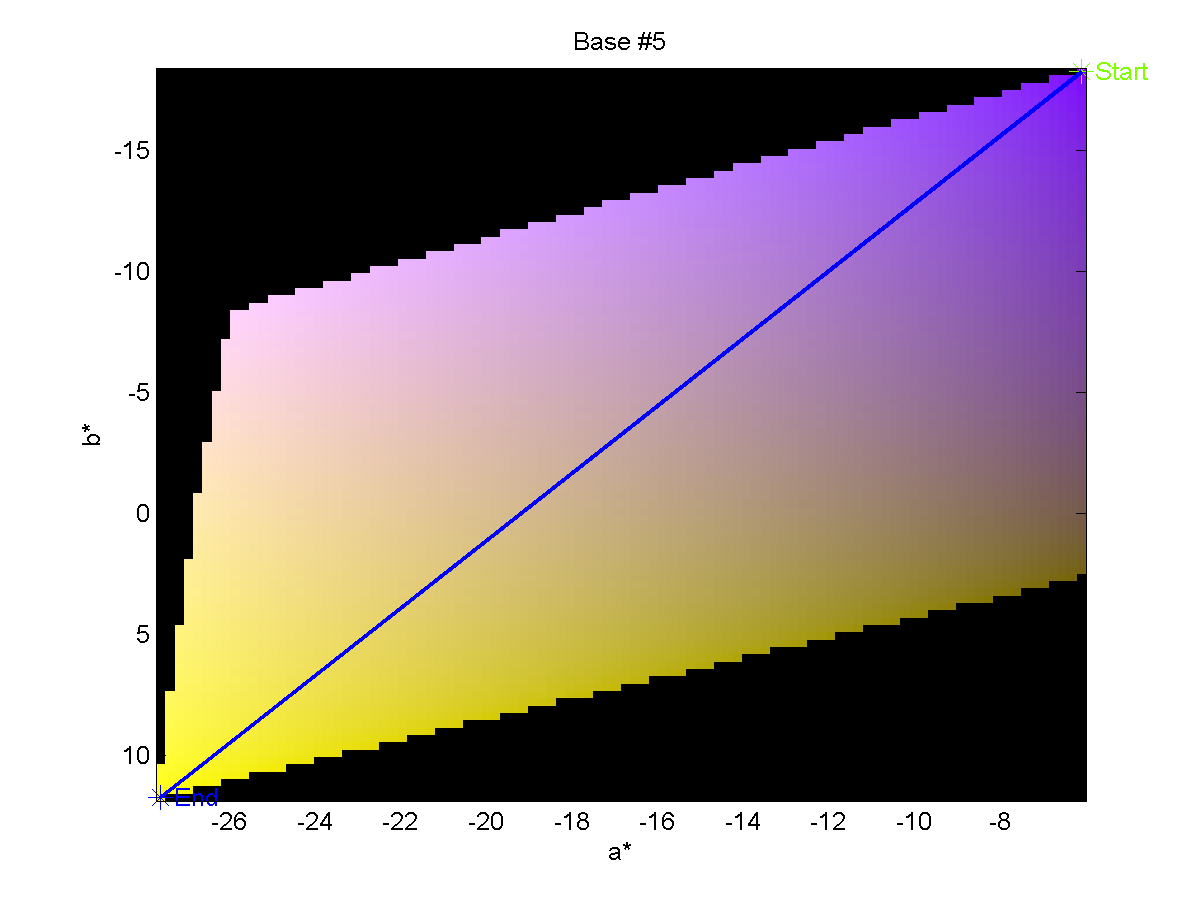
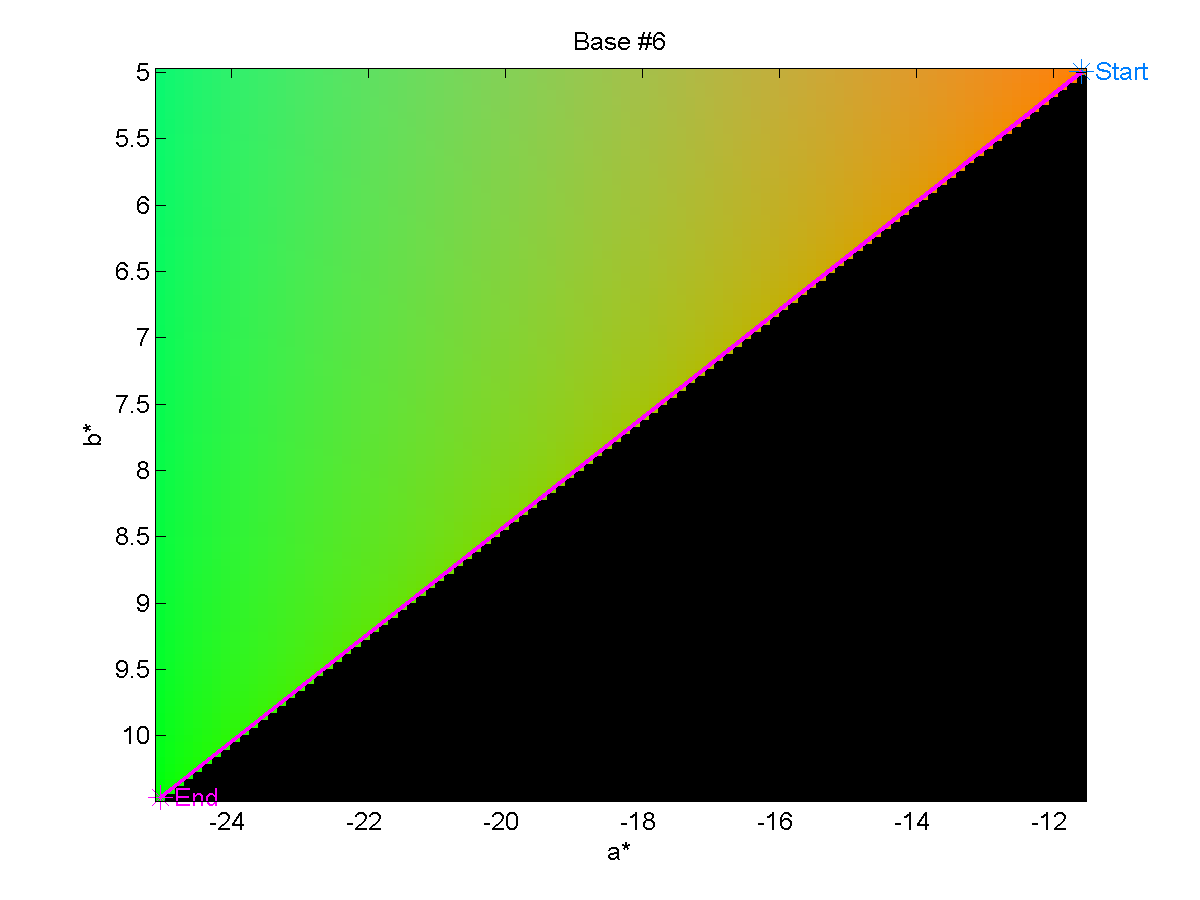
We may also show the paths from the Base to End colors on a planar cut through the CIELAB color space to get a better feel of the space through which we are traversing during the experiment. These images are shown below.


We can also simultaneously plot all of our trajectories through the RGB subset of the CIELAB colorspace, as in the below plot. We can see that our experiment samples a good portion of the RGB space.

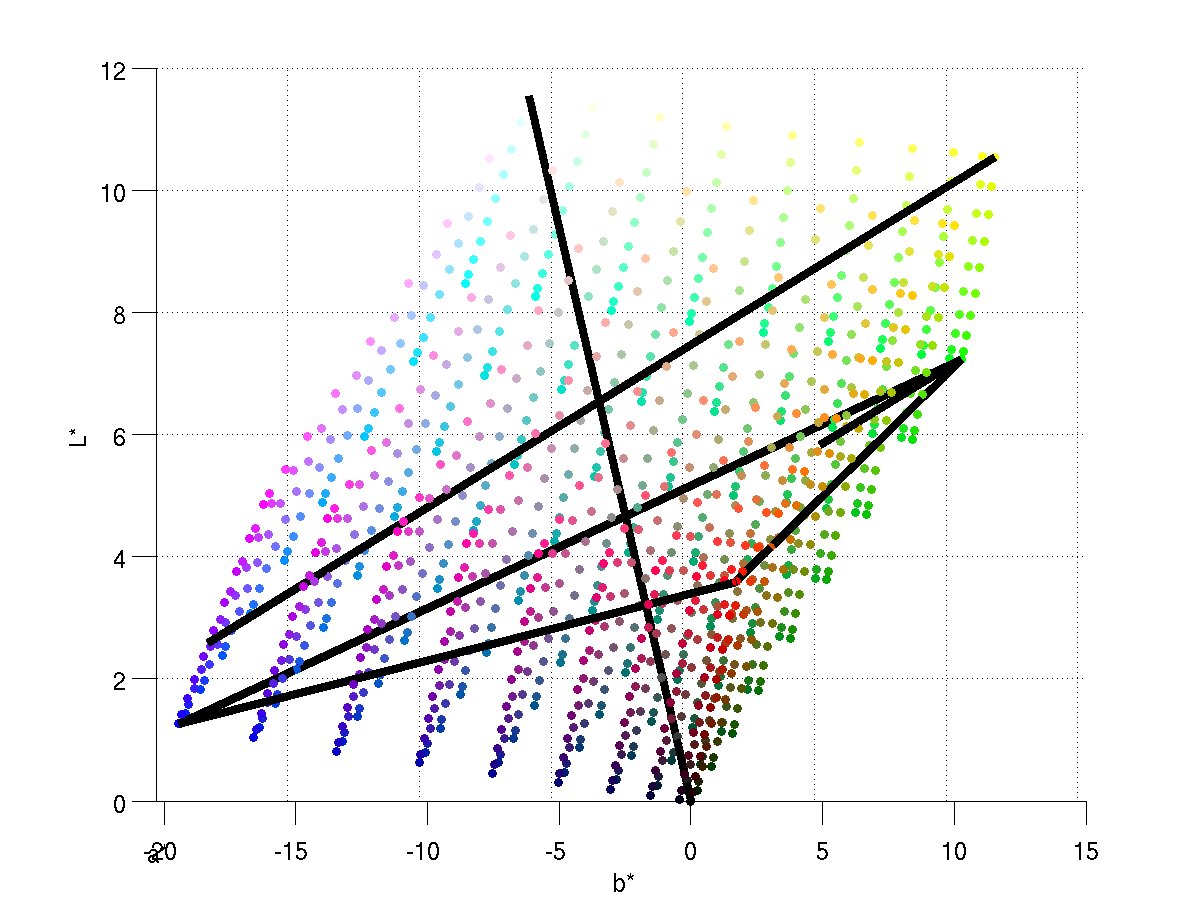Experiment Trajectories through RGB subspace of CIELAB space. The image is projected onto the a* plane.


Subject Information

Seven male graduate students at Stanford University served as subjects for this experiment. Six subjects reported that their color vision was normal and one subject reported Red-Green color-blindness. One subject, who is also one of the experimenters, had previously undergone extensive self-administered flicker photometry testing. Each was given a preliminary training session and was aware of the test objectives.

Results


The results of the experiment were analyzed using Matlab. The code is included in Appendix B.

Staircase Plots

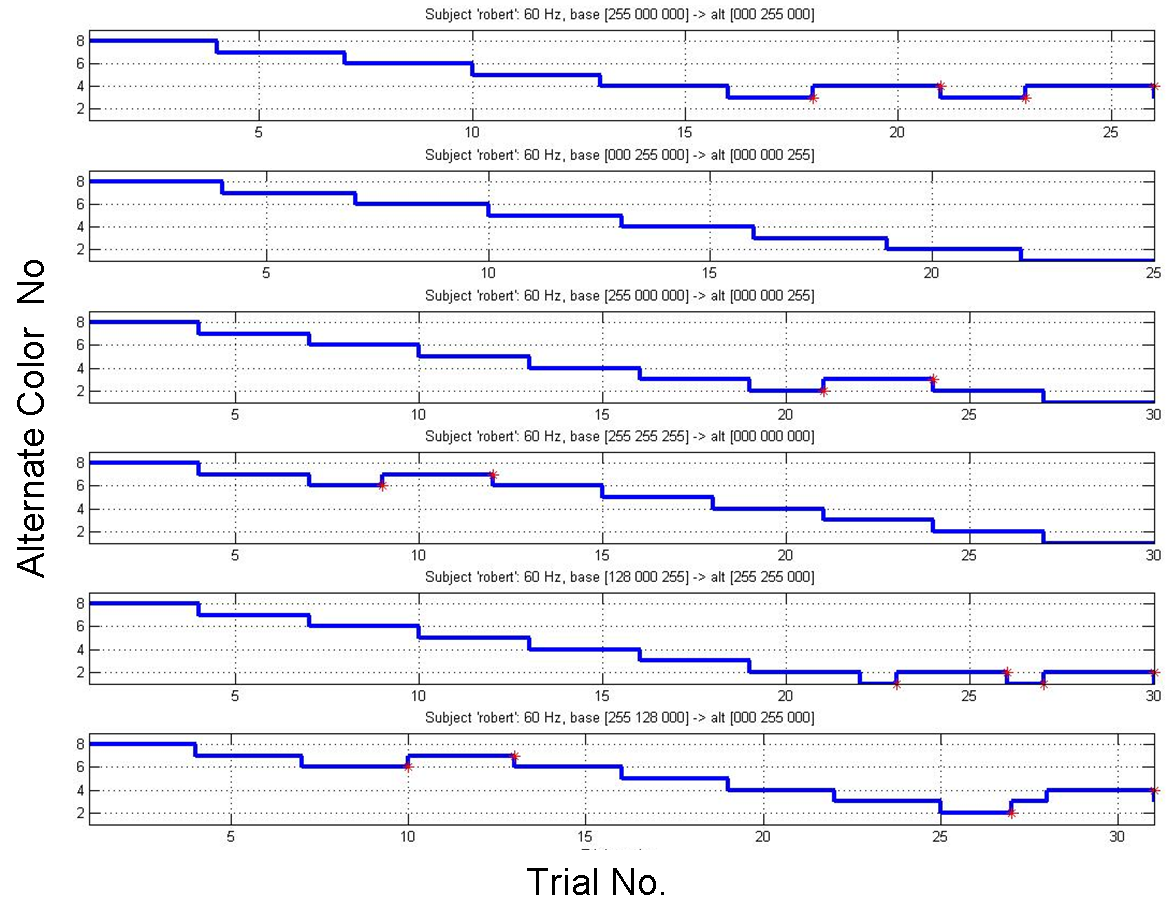
To determine the CFFDs, a staircase plot was produced for each subject. The below figure, for example, shows a typical staircase plot. Each subplot represents the subject's responsiveness to flickering along a single Base/End pair axis. A descent in the staircase indicates that the subject accurately identified flickering three consecutive times and was then shown the base and a closer alternate. An ascent in the staircase indicates that the subject could not accurately identify flickering and was again shown the previous base and alternate. The red markers on the staircase plot indicate reversals, which occur when the subject ascends or descends the staircase to a base and alternate pair that he/she saw in the previous step.




Staircase plot for Subject "RN."

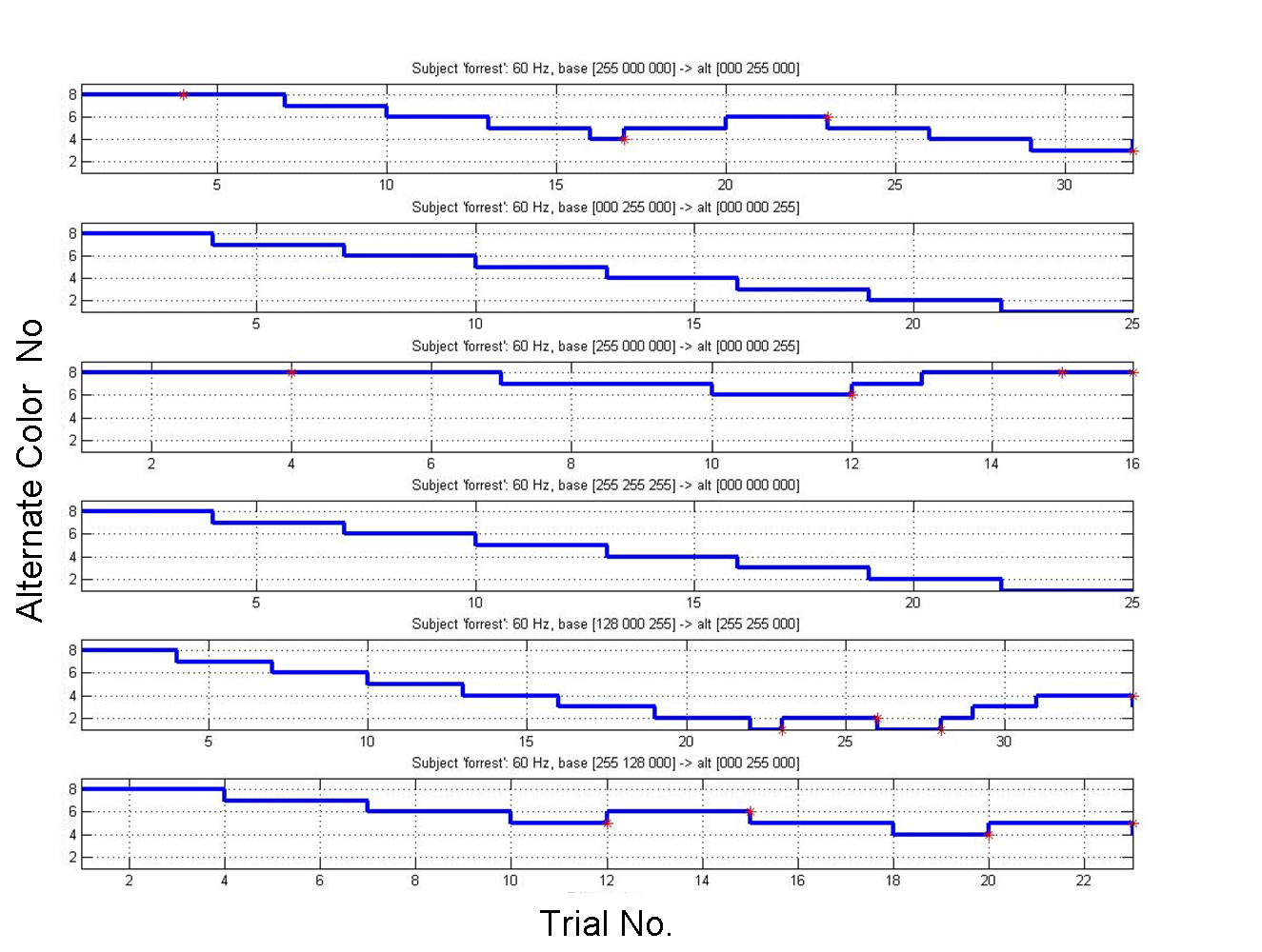
The staircase was designed to give a threshold resolution equivalent to the height of a single step on the staircase. This is because it was assumed that subjects would accrue most reversals between two adjacent steps on the staircase (i.e., oscillate enough times between two adjacent alternates to make it obvious that the threshold lay in between those steps). The results of the experiments, however, showed that many subjects descended the staircase, then ascended again by multiple steps. In the below figure, for example, the uppermost subplot shows that the subject oscillated between steps 4, 5, and 6 for seven steps, then ended the test by descending to step 4. The average threshold for these oscillations does not reflect a resolution of a single step and inherits a large degree of uncertainty.

Staircase Plot for Subject "FF."

CFFD Calculations

The CFFD represents the Euclidean distance between the Base color and the alternate color at the threshold. To determine this value for Base/End pair and from each subject, the threshold step level was first calculated in each staircase subplot. This was done by averaging the staircase levels during at which the four reversals took place. In instances where there were less than four reversals, such as when the user successfully descended the staircase to the last step, the threshold was determined to be the last step. The CFFD was calculated as the Euclidean distance between the base and threshold alternate pair in LAB coordinates:

CFFD = sqrt[ (Lbase - Lalt)2 + (abase - aalt)2 + (bbase - balt)2]

where Lbase, abase, and bbase are the LAB coordinates of the base color and Lalt, aalt, and balt are the LAB coordinates of the alternate color at the threshold.


The CFFDs for each subject and Base/End pair is shown in the below figure. The results show that all subjects were able to descend the staircase entirely for Base/End Pair 4 (White/Black pair), achieving a CFFD of under 10 units. For base/end pairs 1, 2, and 6 (Red/Blue, Green/Blue, and Orange/Green), the subjects all achieved thresholds that were less than 10 units apart from each other, corresponding to two steps on the staircase. One outlier in the results was the Subject "DG" (results marked in light blue). This subject obtained a threshold that was significantly higher than the average for base/end pairs 2,3, and 5. Though we will not make specific conclusions about this subject's results, it is worthy to note that the subject (1) complained of eye dryness due to wearing contact lenses, and (2) has taken the test at least ten consecutive times before so his eyes might have been tired (3) was particularly ornery due to point (2).

 

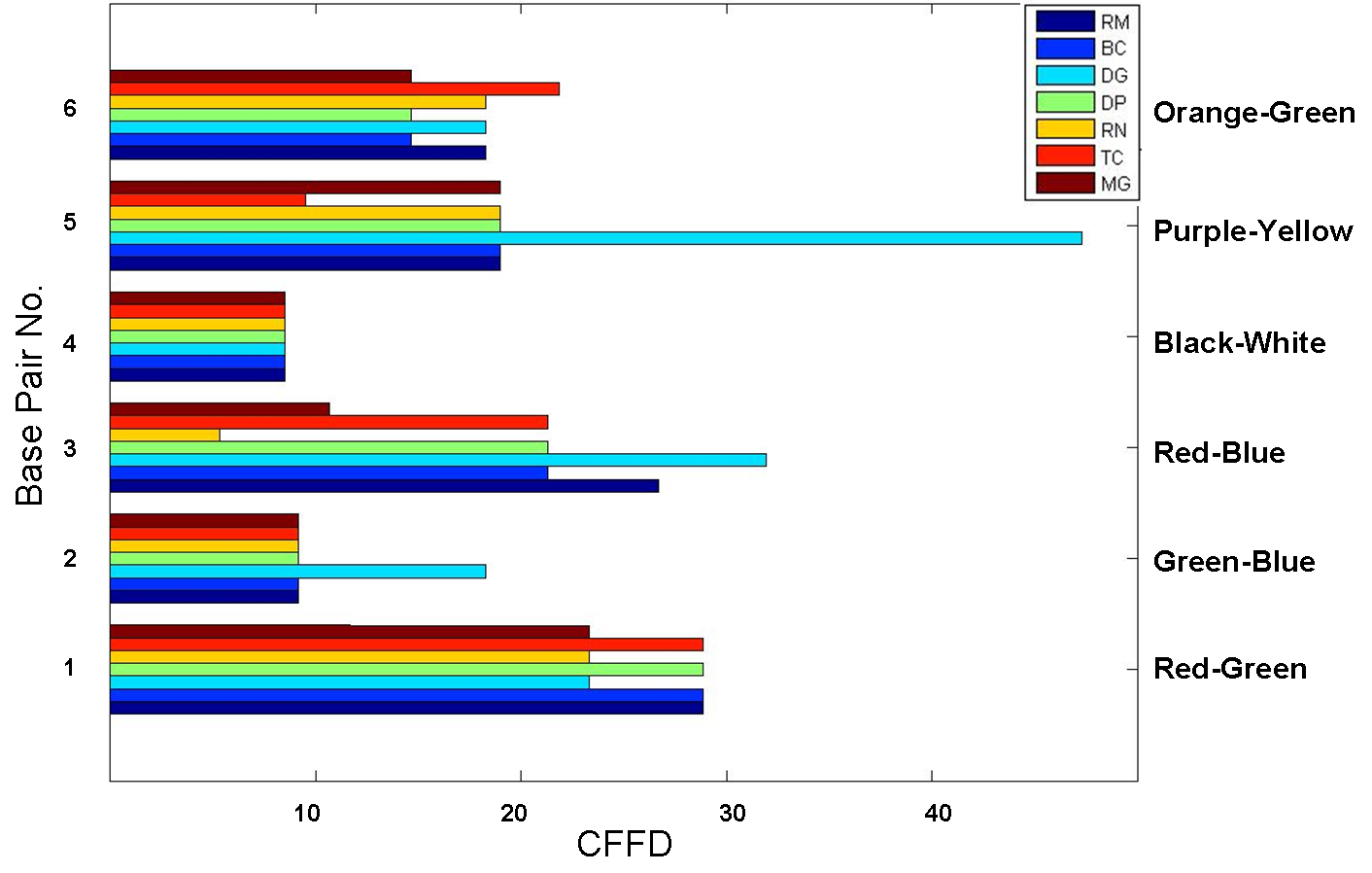
Critical flicker fusion distance (CFFD) for six base/end pairs from seven subjects

 

Subject "TC" (results marked in bright red) was known to have red/green color-blindness. Prior to the experiment, the subject reported difficulty in differentiating red and green colors , but did not have specific information about the degree of his color-blindness or his ability to differentiate between differing levels of luminance. Interestingly, subject TC achieved the same, if not lower, threshold than other subjects in all base/end pair tests, except in the Orange/Green pair (in which his CFFD was higher by less than 5 units). This subject also performed the best in the Purple/Yellow pair test, achieving a CFFD at least 10 units lower than all other subjects.

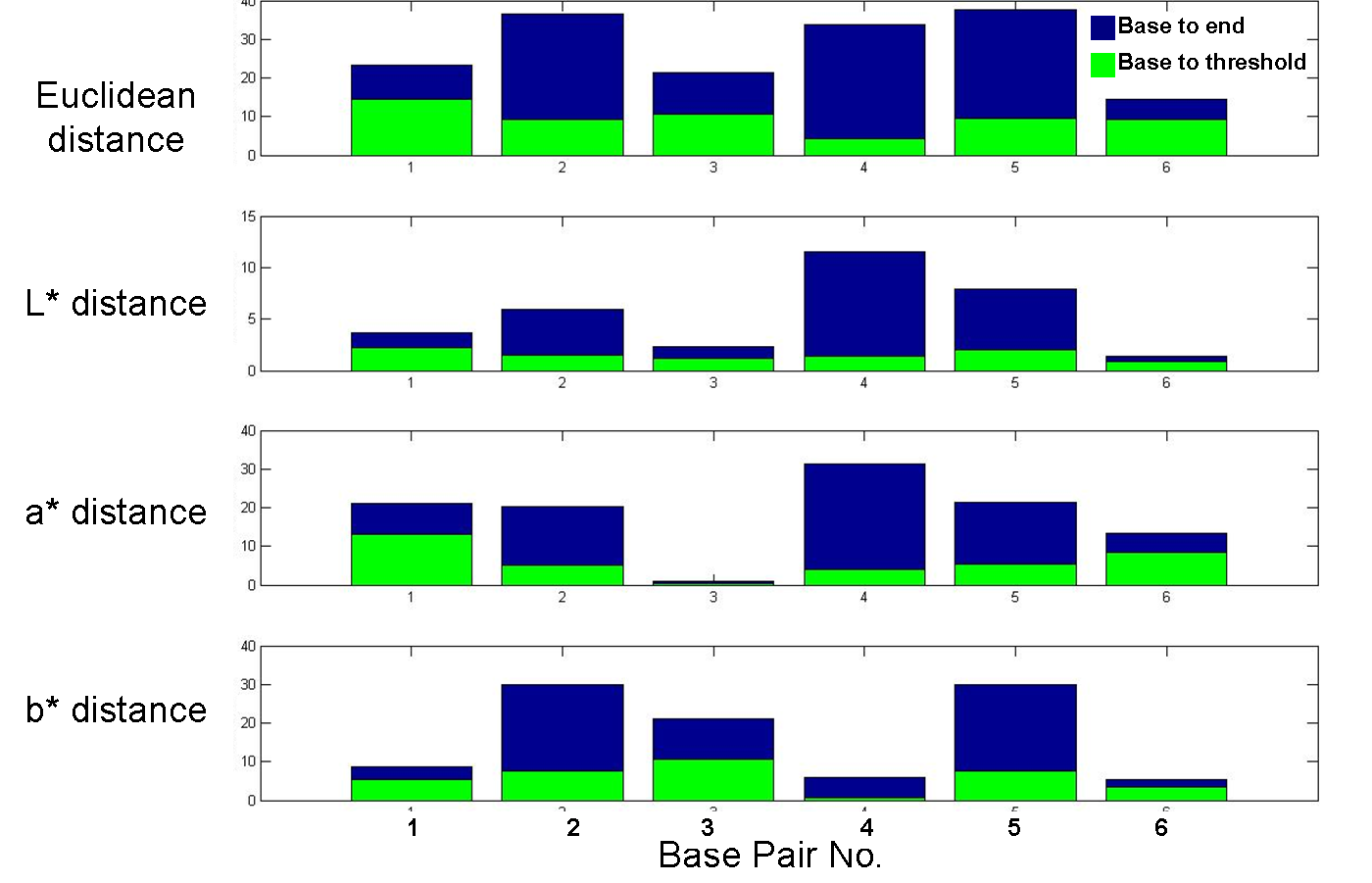
LAB Distances

The below figure shows the differences in LAB coordinates for each base/end pair in blue. The top subplot shows the Euclidean distance between the pairs, and the lower three subplots show the L*, a*, and b* distances between the pairs. The minimum Euclidean distance is between the orange and green pair, and the maximum Euclidean distance is between the purple and yellow pair. The green bars, superimposed on the blue bars, show the Euclidean, L*, a*, and b* distances between the base and threshold colors (averaged over all subjects) for each base/end pair. It is interesting to note that the Euclidean distance between the base and threshold varies in the small range from 5-15 units. In fact, the L* distance between the base and thresholds vary in the even smaller range between 1-2.5 units. The a* and b* distances are not confined to such narrow ranges. These results suggest that the contrast in luminance  (L*) plays the largest role in determining a subject's ability to identify flickering, regardless of where the base and alternate colors exist in the color space. Indeed these results would also explain why the red/green color-blind subject performed normally compared to other subjects if we assume that he does not have trouble differentiating levels of luminance.


L*, a*, and b* distances between base and end colors, and base and threshold colors


Comparison of Results to Previous Work

The results of this experiment agree with previous work in this field. The Ferry-Porter Law, for example, states that the critical fusion frequency (CFF) is proportional to the logarithm of the luminance (L) of the flickering stimulus and can be expressed as

CFF = K logL + C

where K and C are constants (De Lange 1958). This law suggests that flicker fusion perception is most heavily related to luminance (L*), and not as heavily related to chromatic composition (a* and b*). Indeed other studies have shown that under photoptic conditions (in which cones are excited, as opposed to rods), the CFF for lights of different wavelengths with equal brightness also conform to the Ferry-Porter Law and follow the logarithmic function as brightness increases. However, under scotopic levels (when the rods are functioning), the CFF fans out for different wavelengths.

In this experiment, we can assume that we are operating in photoptic conditions since the monitor screen provides adequate brightness and color variations to excite the cones. Thus the results agree with the previous work, showing that contrast in luminance is the greatest factor in identifying flicker, regardless of color.

Conclusions

In this experiment, the critical flicker fusion distance was measured for six pairs of base/end color pairs that spanned the RGB space using 8 subjects. The results showed that the difference in luminance between the base and alternate color matter significantly more than (1) the distance between the base a* and alternate a*, (2) the distance between the base b* and b*, and (3) location of base color in the color space, and (4) direction in color space along which the alternate is chosen.

The results also suggest that Red/Green color-blind individuals will have equivalent ability to identify flickering, assuming that their ability to detect contrast in luminance is not impaired.

Acknowledgments

We wish to thank several members of the Stanford Vision Science and Neuroimaging Group, in particular Bob Dougherty, Joyce Farrell, Kaoru Amano, Serge Dumoulin, and Brian Wandell.

Authors


(Subject SB, who inexplicably developed an ear infection immediately after the experiment)
(Subject DG, whose orneriness during experimentation was later found to be a preexisting condition)

References

De Lange DZN H (1958) Research into the Dynamic Nature of the Human Fovea® Cortex Systems with Intermittent and Modulated Light. II. Phase Shift in Brightness and Delay in Color Perception. J Opt Soc Am 48: 784-789.


Hart Jr, WM (1987) The temporal responsiveness of vision. In: Moses, R. A. and Hart, W. M. (ed) Adlers Physiology of the eye, Clinical Application. St. Louis: The C. V. Mosby Company.


Kelly DH (1974) Spatio-temporal frequency characteristics of color-vision mechanisms. J Opt Soc Amer 64: 983-990.


Truss (1955) Chromatic Flicker Fusion Frequency as a Function of Chromaticity Difference. Journal of the Optical Society of America 47:12: 1130-1134.


Tyler CW and Hamer RD (1990) Analysis of visual modulation sensitivity. IV. Validity of the Ferry-Porter law. J Opt Soc Amer A 7:743-759.

 

Appendix 1: Source Code

Source Code for the experiment can be accessed at http://www.stanford.edu/~dgolden1/sbijoor_dgolden_psych221_final_proj.tar.gz


Appendix 2: Work Breakdown


The work for this project was shared equally by Dan and Sheila, and included: