


Original, Bayer halftoned, and Floyd-Steinberg error diffusion for
the trees image
Below is a matlab continuous color test image entitled "trees". This image was separated into its red, green, and blue components. Both the Bayer halftone matrix and the Floyd-Steinberg error diffusion algorithms were then applied to each color matrix, converting each to values of 0 or 1 for each pixel. The images labeld below show the resulting image when these channels are then recombined.



Original, Bayer halftoned, and Floyd-Steinberg error diffusion for
the trees image
Note that a pixel with both red and green color values of 1 will combine to form a yellow pixel. This combination works the same way in a printer, but in reverse. For example, all red output dots are created from a combination of yellow ink and magenta ink. This model follows the simple subtractive relationship between colors, and does not perfectly hold for actual printers. This is one area real printer pipelines must compensate for. Several way of dealing with this imperfection of ink combination are suggested by model-based halftoning methods [5], [7].
The method separates the RGB color space into Minimum Brightness Variation Quadrants. A RGB color space can be divided into six such quadrants.
The algorithm then works as follows:
Given a pixel value RGB (x , y) and error e (x, y):
-Determine MBVQ based only on RGB (x, y)
-Find closest vertex V of MBVQ tetrahedron to RGB (x, y)
+ e (x, y)
-Compute quantization error = RGB (x, y) + e (x, y) - V
-Distribute error to future pixel error buckets e using standard
error diffusion
A pixel who's original R, G, and B values locate in within the WCMY tetrahedron will end up as one of those four colors, depending on which vertex its error places it closest to.
The algorithm effectively reduces the number of pixel colors visible
in a given solid region. It does not modify the color appearance
when viewed from a significant distance away, however, since it's average
color should remain the same.
A dual level halftoning algorithm can be modified to distribute
values to more than just two potential values. For example, a three
level halftoning algorithm could produce values at 0, 0.5 and 1.0.
Such algorithms are of great use for simulating and implementing printers
with multiple dye levels and/or intensity adjustments such as drops per
pixel or drop size.
The standard halftoning algorithm is modified to run in multiple passes,
with each pass testing between another set of intensity levels. Below
is a diagram illustrating what a enlarged pixel ramp might look like halftoned
over two levels of magenta vs. three levels.
Although it is easy to see the effects of even a single additional color level on halftoning output, there are numerous other ways to try to optimize the combination between levels. However, with increasing level options there is increasing complexity. For example, two levels of each color would produce 48 potential quad color combinations in the above algorithm, rather than six.
Several papers detailing more complex halftoning algorithms fall
under the category of model-based halftoning algorithms. Model-bsed
haftoning follows an iterative procedure that includes effects of a printer
model and an observer model in its halftoning results. Typically,
halftoning results are evaluated using this comprehensive model and factors
are tweaked until the overall error estimated by the model is at a minimum.
Several different variatons can be considered a part of the printer model. One of the first, suggested by Pappas [5], it to take into account any drop overlap between ajoining pixels. Shown below is one such model for this overlap, representing an overlapping drop edge as a partial coloration of that pixel.
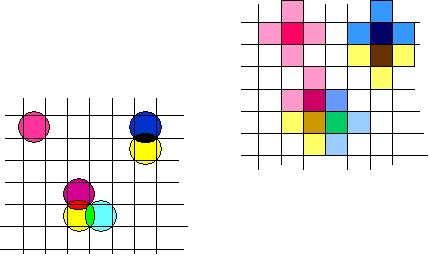
Modeling of inkjet spot overlap as partial pixel coloration
Thi model seems to offer great possibilitiy -- it extendeds the number of possible colors for a pixel significantly -- from 8 where each pixel can have 2 levels each of 3 inks to one major ink contribution plus up to four partial dots -- many more color combinations than could resonably be measured and included. Allebach attempts a similar method based on a 4 drop combination per pixel [7]. Allebach also suggest a clever way to calibrate color results for a hlftoning process based on a set of 1072 measurements of these combinations included in a YyCxCz map of the printer's color gamut.
The second part of the model is meant to account for the human visual system. Allebach uses the pointspread function convolved with the dot profile to estimate the overal shade contribution to each pixel. This overall effect is factored into an error function. Trial pixel changes are each tested under this model until the error is seen to be minimized, though the complexity of this caculation is large, and the variations numerous.
Although these models take into account many interesting aspects of
printer and visual system behavior, they do not seem to offer a practical
use for efficient desktop printer use. They do, however, offer some
insight into ways to develop halftone weighting factors and color calibration
methods for halftoning in offline development where comutation time is
less of an issue.
Continue to Results
Return to Index