Julesz first realized that the first-order statistics (color histogram) cannot help to get the visual structure because it is invariant to pixel permutation. Since vision is primarily concerned as relationship between colors across space and time, the dipole may be a useful tool. Doner has argued that

Human sensitivity to some aspect of spatial pattern is reflected by various measures of dipole histogram entropy

Nonetheless the dipole histogram would be of limited value if it can't be uniquely determined from an image.

• Dipole Histogram Uniqueness Theorem

  Any finite two-dimensional image I is uniquely determined by its dipole histogram.

  Any finite, discrete, two-dimensional image I comprising M+1 rows and N+1 columns can be constructed using only those of its 'short' dipoles; i.e. those dipoles (dy,dx) with |dy|<=ceil((M+1)/2) and |dx|<=ceil((N+1)/2).

  Definition of Dipole Histogram:

  D(dx,dy,a,b)=number of pairs [(x1,y1) (x2,y2)] such that

  I(x1,y1)=a and I(x2,y2)=b and (x2,y2)-(x1,y1)=(dx,dy) where a,b are intensity values

  Apparently D contains no locational information

  Proof:
  S(m,n)=sum D(m,n,a,b)*a;     for a=0:L-1, b=0:L-1     L:intensity value

  S(m,n)=sum D(m,n,a,b)*a=sum I(x,y)*I(x+m,y+n) for x=M-1-m, y=N-1-n

  I(m,n)=S(m,n)-S(m-1,n)-S(m,n-1)+S(m-1,n-1);

  By this algorithm, all I(m,n) can be generated

  The second algorithm can also be easily shown by divide the whole image into four quadrants and use the D(m,n,a,b) for (|m|,|n|)<=ceil(M/2,N/2)

  Actually the 2 reconstructions are equivalent. The first uses D(m,n,a,b), (m,n)=(0:M-1,0:N-1). The second one uses (|m|,|n|)<=ceil(M/2,N/2)

  The two versions of Dipole Histogram Uniqueness Theorem are implemented as reconstr.m and reconstrHalf.m

  A coin-flip image has been chosen to show the correct reconstruction of the algorithm

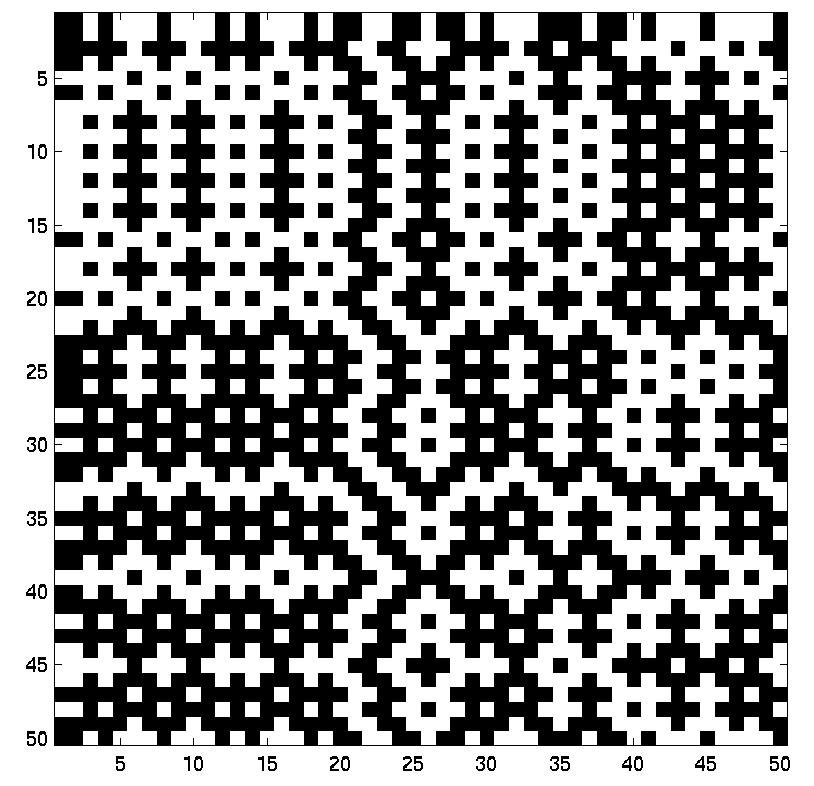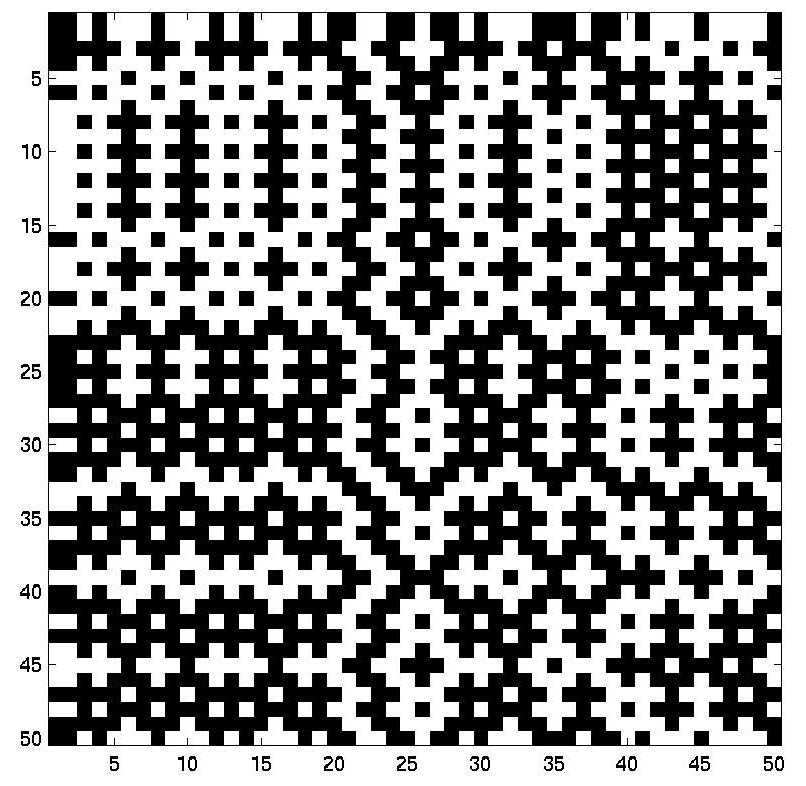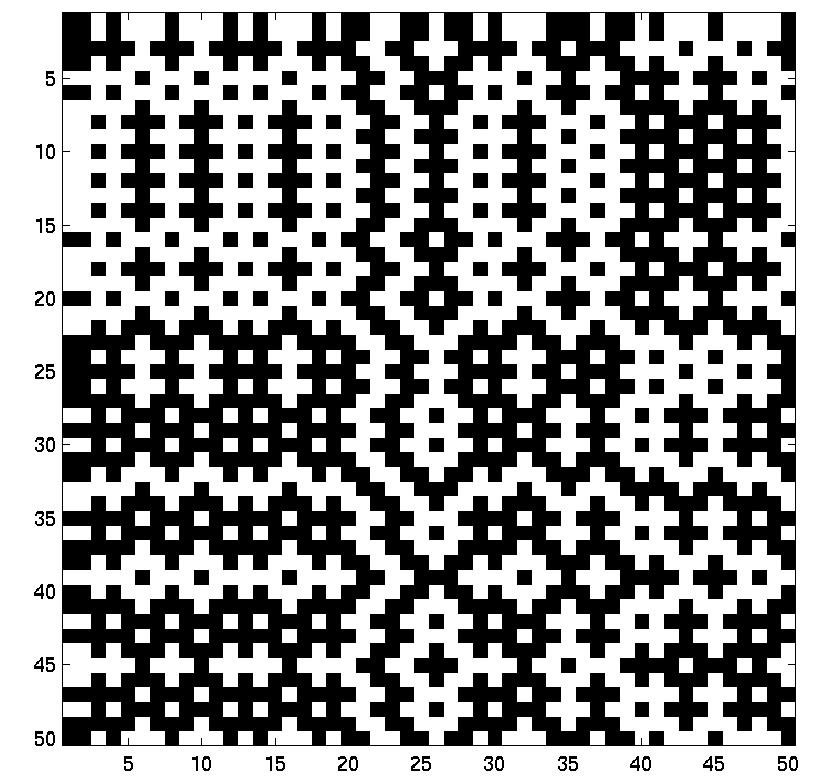  Original	Reconstructed by dipole range 0:M-1	Reconstructed by dipole -ceil(M/2):ceil(M/2)

  The reconstructed images have been examined by Matlab to be the same as the original.