Results

Implementation Results

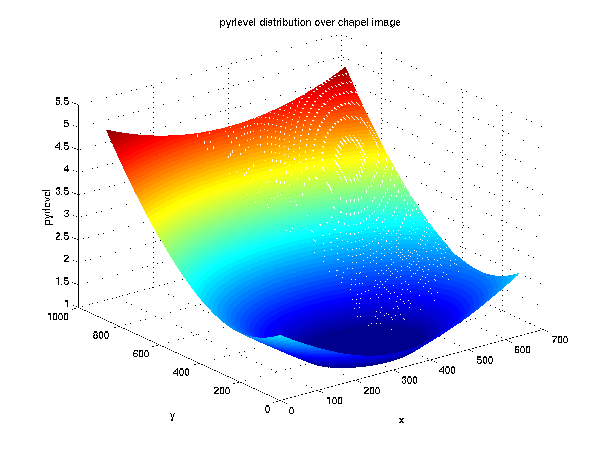
In order to generate foveated images, the MATLAB script foveate.m was used. As an example, consider the large high-resolution image in Figure 4. First, the degree of foveation was calculated for each point within the image. This was done as described in the Implementation section above. The resulting pyrlevel matrix is shown three-dimensionally in Figure 5.

This distribution was calculated using a focal point near the top of the image, at a viewing distance of 0.3 meters (about 1 foot). In the central fovea, this distribution was truncated due to the finite resolution of the monitor compared to the resolving capabilities of the eye. The maximum value of pyrlevel was just above 5, indicating that a six-level pyramid is sufficient to foveate the full extent of the image. If fewer pyramid levels are desired, the maximum value of the pyrlevel structure must be limited to the number of pyramid levels actually computed.

Figure 5: Meshplot of pyramid level versus location within image. Pixels further from the central fovea are rendered from a higher pyramid level.

Next, this pyrlevel structure was used to generate a foveated image. In the literature, the most common approach to this is to use a floor operation to convert level numbers from the pyrlevel matrix into integers. An example using such an approach is shown in Figure 6. While this approach is computationally efficient, the ring artifacts around each step boundary are quite noticeable. Even when fixating on the correct point of gaze as calculated for the image, the ring artifacts are noticable in the peripheral vision. In order to reduce this effect, interpolation between pyramid levels is necessary.

Using linear interpolation between pyramid levels, Figure 7 was obtained. In this image, there are no step discontinuities, and the blurring appears to uniformly increase away from the foveation point. The disadvantage of this technique is that it requires much more computation time.

Several images resulting from the fully implemented algorithm are shown in Figures 8-12.

Figure 8
Figure 9
Figure 10
Figure 11
Figure 12

This technique is not limited to single-fovea images. Figure 13 shows an image which was foveated using two foci of gaze. This was implemented by computing two separate pyrlevel matrices, and at each pixel in the image, the lower of the two pyrlevel values was used.

Figure 13: Example of image calculated using multiple foveae. Two distinct centers of gaze are present, one on each banner. The foveation parameters used here were increased in order to accentuate the effects of such foveation in a small image.

Compression through Foveation

Compression of images was achieved by saving the required data for the above reconstructions as a Laplacian pyramid. Laplacian.m is a MATLAB script which saves the necessary foveated data as a compressed Laplacian pyramid.

The color YCbCr data from each level of the Laplacian pyramid were converted back to RGB and then quantized into 8-bit integer values before writing (24 bits per pixel), and the result was compressed using the gzip utility. The resulting image files were compared in size to files which were prepared identically except that information for the entire pyramid was saved instead of just the foveated regions.

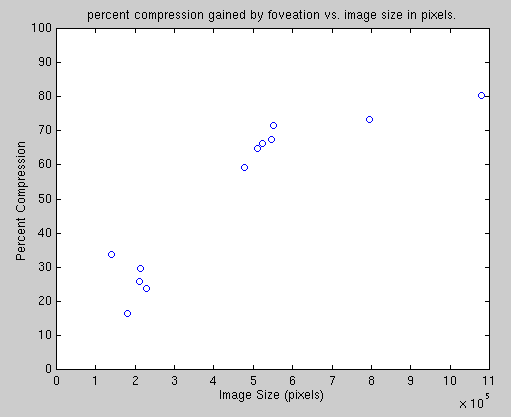
In general, foveation produced significant storage savings over standard Laplacian pyramid compression. Figure 14 shows percent compression when compared to standard Laplacian pyramid encoding for twelve images. As the figure shows, gains in compression were highly correlated with the size of the image to be encoded. For large high-resolution images, compression ratios exceeded 80%. For image sizes which are typical on the web today, compression ranged from 20-30%. In these cases, the compression ratio was more strongly dependent on the exact placement of the point of gaze.

Figure 14: Compression gained as a result of foveation for 12 images. Percent compression values are computed by comparison with uniform-resolution images stored using Laplacian pyramid encoding and gzip compression, as discussed in the text.

Fovea-First Transmission

Since the storage requirements for fovea-first images are virtually identical to those for uniform-resolution pyramidal encoding, compression ratios were not calculated in these examples. The goal of this technique is to provide successive image transmission which provides a foveated view of the image first, then transmits the rest of the image.

An example of such a progressive image transmission strategy is shown in Movie 1. This movie shows the progression of image quality throughout the transmission process. In order to depict the effect more dramatically, the foveation was emphasized and is not meant to reflect the variation in resolution of the human visual system. This movie also does not account for the transmission times required for each level of the pyramid. Each frame of the movie is on screen for the same duration, even though there may be very little data transmitted during some frames.

Another example of fovea-first successive image transmission is shown in Movie 2. These movies show that in certain applications, foveated successive image transmission can be useful in highlighting regions of interest as quickly as possible.

Bill Overall / March 12, 1999