

Approaches to Foveation
When rendered on the screen, foveated images take up as many pixels as
unfoveated images. Therefore, to realize any data savings from
foveation, some algorithm must be used to generate the full image from
a reduced data set. In the literature, there appear to be four broad
implementation approaches.
One approach that has been used is to directly warp the image using
one of a number of nonlinear operations. Wiebe and Basu describe a
host of these algorithms. Most of these methods result in
compressed images with oddly-shaped boundaries, which are often
difficult to transmit and decode in a standard way.
In addition, many of the resolution functions used have singularities
at the fovea, meaning that special processing must be used in the
area of highest fidelity. Finally, these algorithms become even more
difficult to implement if the fovea does not lie at the image center.
Because of their inflexibility, these algorithms are seldom
used for general-purpose image foveation.
A second approach found in the literature (see, for example, Tsumura
et al.) is the use of variable-quality DCT compression. In standard
block DCT compression, a single quality factor is set for the entire
image, and the image is uniformly degraded by that factor. To
"foveate" such an image, the quality factor is allowed to vary for
each 8x8 DCT block. At blocks close to the fovea center, the quality
factor approaches 100%. As blocks get further from the fovea, the
quality factor decreases in proportion to visual acuity. Since lower quality
factors generally mean that higher spatial frequencies will be
represented more poorly, the net effect is to reduce spatial
resolution away from the fovea. The maximum degradation is
constrained by the size of the DCT blocks. While this approach shows
promise, it is unclear how the spatial sensitivity of the human visual
system can be correlated with DCT quality factors. Block boundary
artifacts also become a problem at locations far from the fovea.
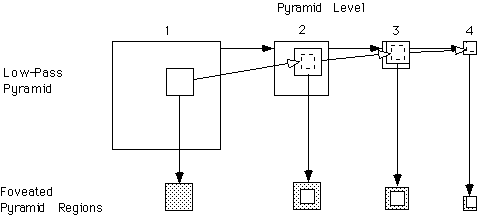
Geisler and Perry have proposed the use of an image pyramid representation for foveating images. In a standard image pyramid, as described by Burt and Adelson, the image is blurred and subsampled repeatedly to create a number of copies of the original image at different resolutions. In a foveated approach, the image pyramid represents less and less of the image as it reaches the top. Figure 3 shows a standard pyramid representation with subsets removed from each level of the pyramid for foveation.
This manner of image decomposition lends itself to fovea-first transmission. If the foveal regions of the pyramid are transmitted first, then the remaining data can easily be transmitted later without any redundant data transmission. A very slight penalty will be paid over the unfoveated pyramid transmission in order to transmit the coordinates of each foveation subregion.
Finally, there has been a proliferation of literature in recent years attempting to use various wavelet transforms in order to foveate images. Mallat describes the general form of wavelet decompositions, which are very similar in spirit to the multiresolution pyramid approach. Using wavelets, an image can be decomposed into four child images, each of which is one quarter the size of the original. These four images can be used to fully recreate the original. The advantage of this approach over the Laplacian pyramid is that no redundant information is added in order to build the pyramid. At each level of the wavelet pyramid, four subimages are created which represent the low- and high-frequency components of the image in each of the two dimensions. Therefore, those portions of the high-frequency subimages that are far from the fovea need not be transmitted. This approach has been studied by Chang and Yap, as well as Dreizen. Bandwidth reduction is again achieved by sending only data which can be resolved by the viewer. This approach can also be easily modified in order to accomodate fovea-first transmission.
Foveal Resolution Functions
Regardless of the image decomposition strategy which is employed, the algorithm must determine which resolutions are appropriate at each point in the transmitted image. A function must be used which approximates the spatial response of the human visual system. The literature describes several such functions.
Schwartz studied the signals mapped onto the visual cortex and determined that a logarithmic resolution function would be most appropriate. Though this function is biologically-based, its implementation is difficult due to singularities along one axis. Therefore, simplifications of this algorithm abound. Wiebe and Basu describe an array of variable resolution transforms designed for ease of computation and storage.
Geisler and Perry use a variation on Schwartz' resolution
function which seems to have been well-explored in the literature.
The function is
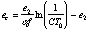 (1)
(1)Using this formula, Arnow and Geisler found that the best fit for humans occurred with alpha = 0.106, e2 = 2.3 degrees, and CT0 = 1/75. Other researchers have published similar results.
