Tsai and Huang Frequency Domain Method (2D)

Most of the processes presented in the 1D case map directly to the 2D case.  This is largely just an extension of the general method to include another dimension.  As before, where at all possible, we have maintained the identity of the variables used in the paper (except for where they just drove us absolutely crazy.)
 

1)  Definitions

(x,y)       = real-space coordinates
(u,v)       = frequency-space coordinates
f(x,y)      = ideal image
= ideal image shifted by (, ) = 
p            = number of frames
      = (i,j)th sample in the kth frame

M           = numberof samples in each frame in x-direction
N           = numberof samples in each frame in y-direction
          = sampling interval in x-direction
          = sampling interval in y-direction
        = inital offset of kth frame in x-direction
        = inital offset of kth frame in y-direction
F(u,v)     = Continuous Fourier Transform (CFT) of continuous signal f(x,y)
= CFT of shifted continuous signal 
        = sampling frequency in x direction = 1/
        = sampling frequency in y direction = 1/
        = (m,n)th component of the DFT of the kth frame (i.e. (m,n)th component of DFT of )
          = resolution improvement factor in u
          = resolution improvement factor in v
J             = our complex number, not i, not j, because those are used extensively in this paper for other things

Note, by definition, if k[0,p-1], then 
Also note that i[0, M-1] and j[0,N-1]
 

2)  Method

Again from continuous Fourier Transform (CFT) theory there is a simple way to relate shifted functions to non-shifted functions:
             .
where F(u,v) is the continuous Fourier Transform of the ideal image f(x,y).  In images,however, we desire to look in discrete space, so we need a way to relate this to disrete variables.  We have for this, the Discrete Fourier Transform (DFT),
             .
We note here that n[0,N-1] and m[0,M-1].  We now have p DFT matrixies of size MxN.  Note k{0,p-1}

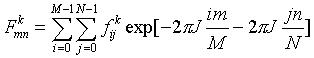
Now we relate the DFT to the CFT with the 2D version of the "aliasing relationship":
             .
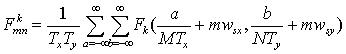
So we have now related each discrete component, that is the (m,n)th frequency component shifted by k, to the continuous representation shifted by k.  This again becomes important.

Again we make the assumption that F(u,v) is bandlimited in both directions.  We do this by saying that F(u,v) = 0 for all w such that |u| >  *  and |v|>*

This enables us to write another matrix equation:
              .
We will not draw the matricies together as we did last time.  We will now however, examine each matrix individually.

.....beginning with

              .

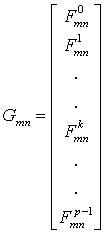
so  which we already know from the DFT.  This vector is of length p.

Now we look at........
              .
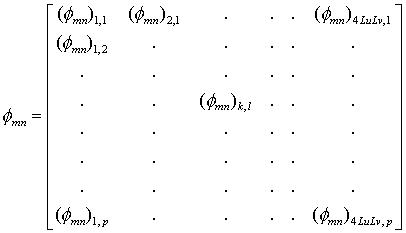
where
              .
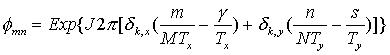
so we see that this too is something we can readily calculate.  This matrix is of size p x 4

In this paper, methods are desribed to circumvent the direct calculation of both of the above matricies.  As we will now see, we desire to find the values of , which can be obtained more readily by noting some symmetries of the above matricies.

Now we look at.......
              .
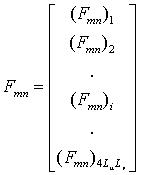
where
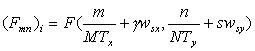              . which we note is a relation bewteen the CFT at a given point in
                                                                               continuous space and values from the DFT.  This vector is
                                                                               4 in length
              .

              .

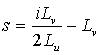
and we now see that we can calculate exatly the continuous (u,v) coordinate at which to put the value 
 

Note that  is a  matrix containing 4 points.  We have not yet determined the values of  and .

Once we have solved this matrix equation, what do we do now?  We have values for this matrix , but what do these numbers mean?  As with in the 1D case, these are values of the continuous Fourier Transform at a given (u,v) point
             .
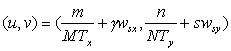
So we have taken these 4 values and assigned (u,v) coordinates to them in the frequency domain as sample point of the frequency representation of the continuous ideal image.  Now again, the matrix equation above considers only the (m,n)nth component of all p of our DFTs.  We have (N-1)(M-1) more matrix equations to solve, and thus 4(N-1)(M-1) more points to add to our frequency representation of the continous ideal image.  In total, we will have 4MN points in our representation, whereas we started out with MN (being the most points we could obtain from any one image.)  So we see that our resolution has increased by a factor 4!  If we want a resolution increase of 2 in each direction (and thus 4 overall), we make ==1.  In general, we will use small-ish values of L.

Of course, in order to recover the exact image exactly, we would need enough points to be above the Nyquist frequency with respect to the variations of the signal as it reaches the "camera".  Nonetheless, we know that the more points we add to the bandlimited frequency representation, the more accurately we will be able to determine the signal in the space domain.

Once we have finished mapping all points from all n into frequency space, we use an 2D inverse Fourier Transform to obtain our higher resolution image.