vision

Demosaicing of a Color Filter Array

Validation of the "Acharya & Tsai" Algorithm

John MacMahon

Psych221

Winter 1999

What 3 things do we look for in a Color Digital Camera?

BETTER

FASTER

CHEAPER

Meanwhile as engineers we look at the above tasks and say pick any two!

What does the perfect camera have?

A heads up display

An onboard Pentium 3 for high speed work

3 independent RGB sensors coordinated controlled with gyro stabilized prisms

and a Cup holder

How about the cost of such a camera?

Well the cost of the sensors alone are between 10 & 25% of the entire cost of a camera(Adams, et al.).

The color filtered array (CFA) addresses the CHEAPER aspect for the consumer. The CFA attempts to use a single array of detectors with an organized pattern of filters (RGB) on each pixel to get performance from 1 array instead of 3.

A common CFA pattern is called the Bayer.

R	G	R	G	R
G	B	G	B	G
R	G	R	G	R
G	B	G	B	G
R	G	R	G	R
G	B	G	B	G

CFA - Bayer Pattern

This scheme results in 25% Red and Blue coverage and 50% Green coverage of the array. This results in an image that is a "mosaic" of 3 colors and continuous in none.

Now if one is to output a 512 x 512 RGB image then color interpolation must occur for the missing values. This is the "demosaicing" of the image.

Now we have accomplished reduced cost, but how much has the image quality degraded? There are many approaches to solve this problem (Adams, 1995 and Freeman, 1988).

Acharya and Tsai recently proposed a new block matching based color interpolation algorithm. This algorithm will be introduced by example.

Definitions:

Color Block - The 4 adjacent Green pixels around a non-green pixel

Color Gravity - the mean of the color block

D G's - Absolute differences between color gravities

Directions: N,NE,E … Top, Bottom …

Coded Example:

While Sitting on a Red Pixel:

R	G	R	G	R
G	B	G	B	G
R	G	R= 18	G	R
G	B	G	B	G
R	G	R	G	R
G	B	G	B	G

CFA - Bayer Pattern

R= 18

This pixel of course get its own red value.

Its G value is the median of its color block.

Median ( 18 , 12, 10 , 10) = 11

Gravity (Mean(block)) = 12.5

R= 18

G= 11

Grav.=12.5

The green value to go with the red in the center is thus 11.

R	G	R	G	R
G	B	G	B	G
R	G	R= 18 G= 11 Grav.=12.5	G= 12	R
G	B	G = 10	B(SE) Grav.=14	G = 20
R	G	R	G = 14	R
G	B	G	B	G

Now what to do for a blue value.

Looking at the highlighted Blue(NE) it has a quartet of neighboring greens that will make up the color block for this SE blue pixel.

Blue(NE) block = (12,20,14,10)

Blue(SE) gravity = mean(block) = 14

Gravities (means) of this and the other 3 blues blocks that surround our central red will then be calculated.

So we now have 5 blocks: 1 in the center, and those that go with the Blues at the NE,SE,SW,NW blocks.

R	G	R	G	R
G	B(NW) Grav.=18	G	B(NE) Grav.=15.5	G
R	G	R= 18 G= 11 Grav.=12.5	G	R
G	B(SW) Grav.=16	G	B(SE) Blue = 15 Grav.=14	G
R	G	R	G	R
G	B	G	B	G

Now the delta_G's are calculated.

D G(NE) = abs(12.5-15.5) = 3

D G(SE) = abs(12.5-14) = 1.5

D G(NE) = abs(12.5-16) = 3.5

D G(NE) = abs(12.5-18) = 5.5

The minimum D G points in the SE direction.

The direction of the lowest delta-G determines which Blue pixel is copied over to become the missing blue value to join the Red and the calculated Green of the center.

R	G	R	G	R
G	B	G	B	G
R	G	R= 18 G= 11 B = 15	G	R
G	B	G	B	G
R	G	R	G	R
G	B	G	B	G

This pixel is now done.

A bit tricky to explain, but doable. If you are on a blue pixel the process is similar.

Motivations?

Cost - Speed?

If you are on a green pixel though…

R	G	R	G	R
G	B	G	B	G
R	G	R	G	R
G	B	G	B	G
R	G	R	G	R
G	B	G	B	G

How to get the blue and red

Now there are blues above and below, each of these has a color block. Instead of 4 block there are only 2. The D G's are checked. Lowest value wins and, this is done across the rows for the red value.

Results:

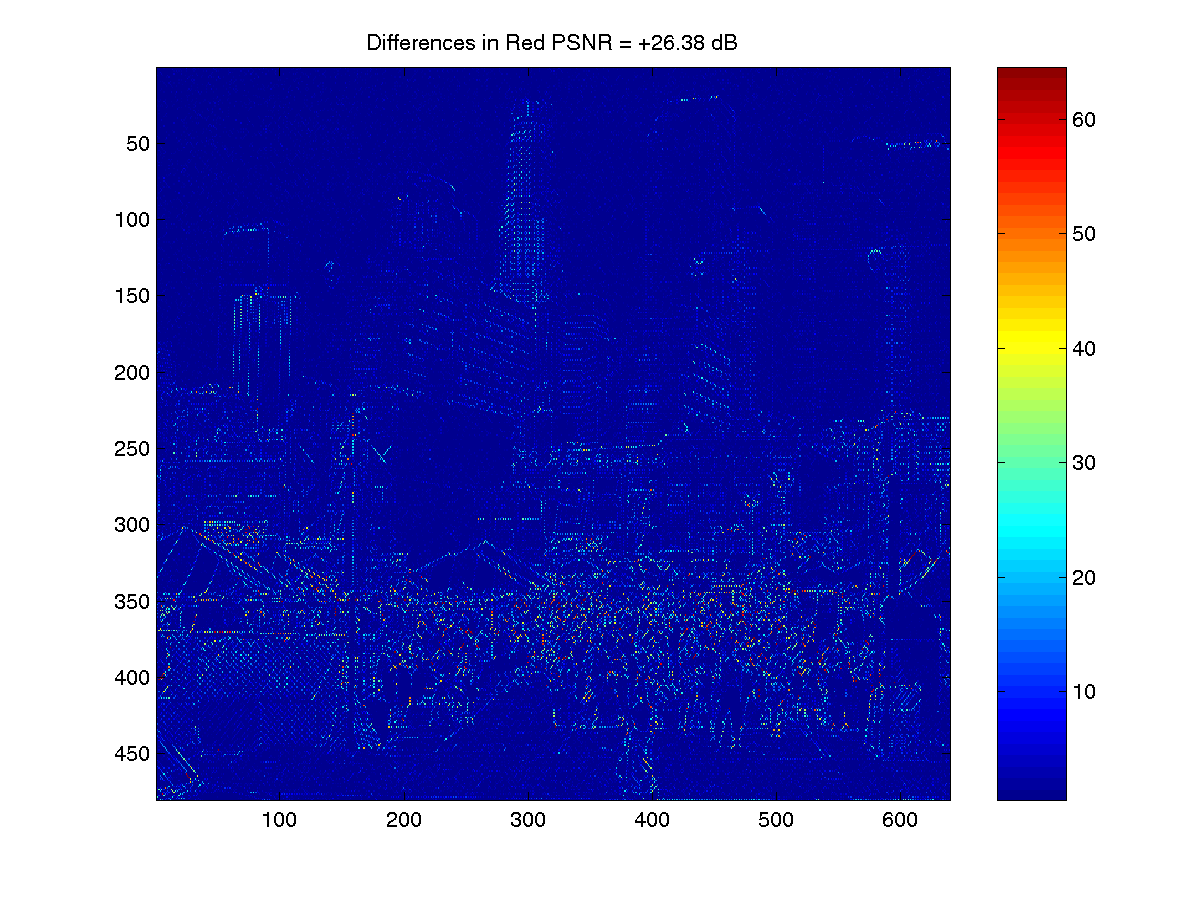
Difference b/t Original and Block Matched Interpolation (Red)

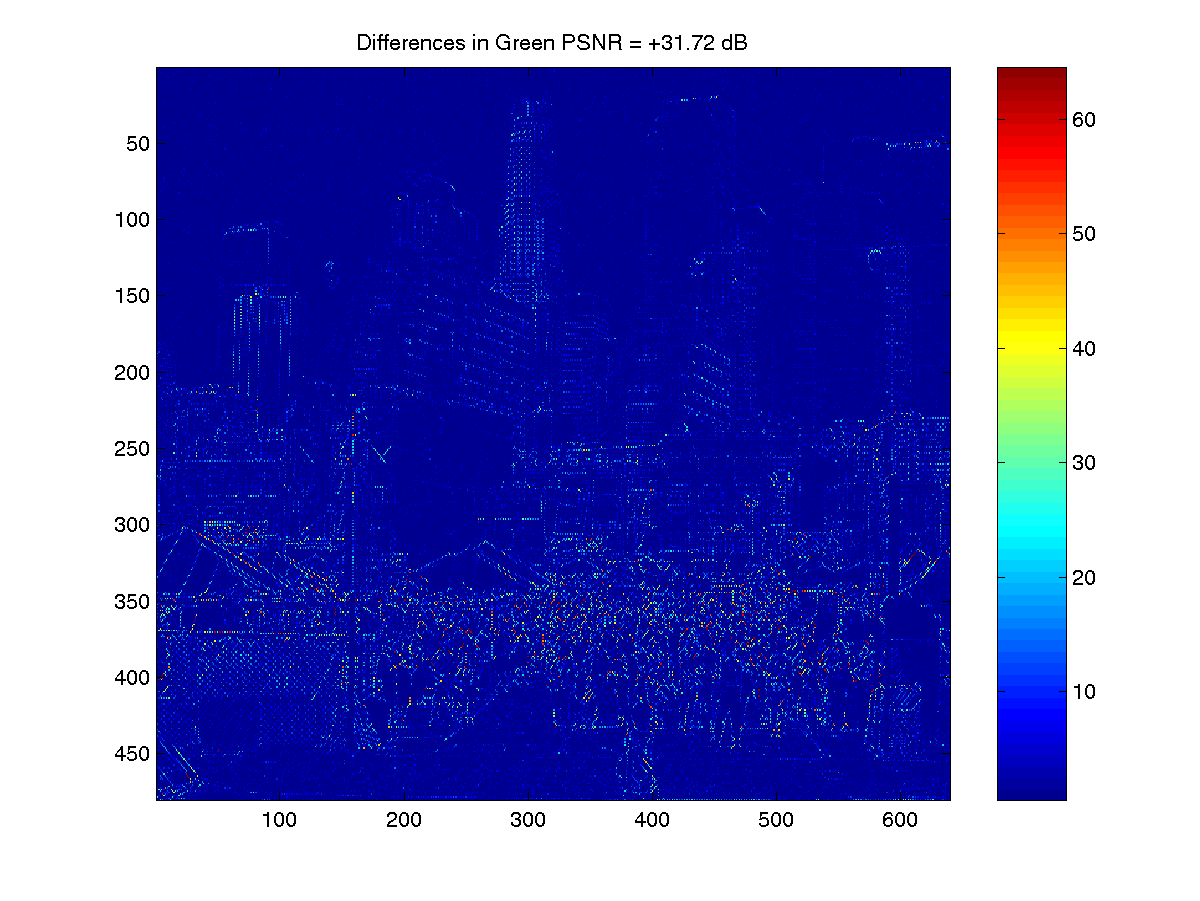
Difference b/t Original and Block Matched Interpolation (Green)

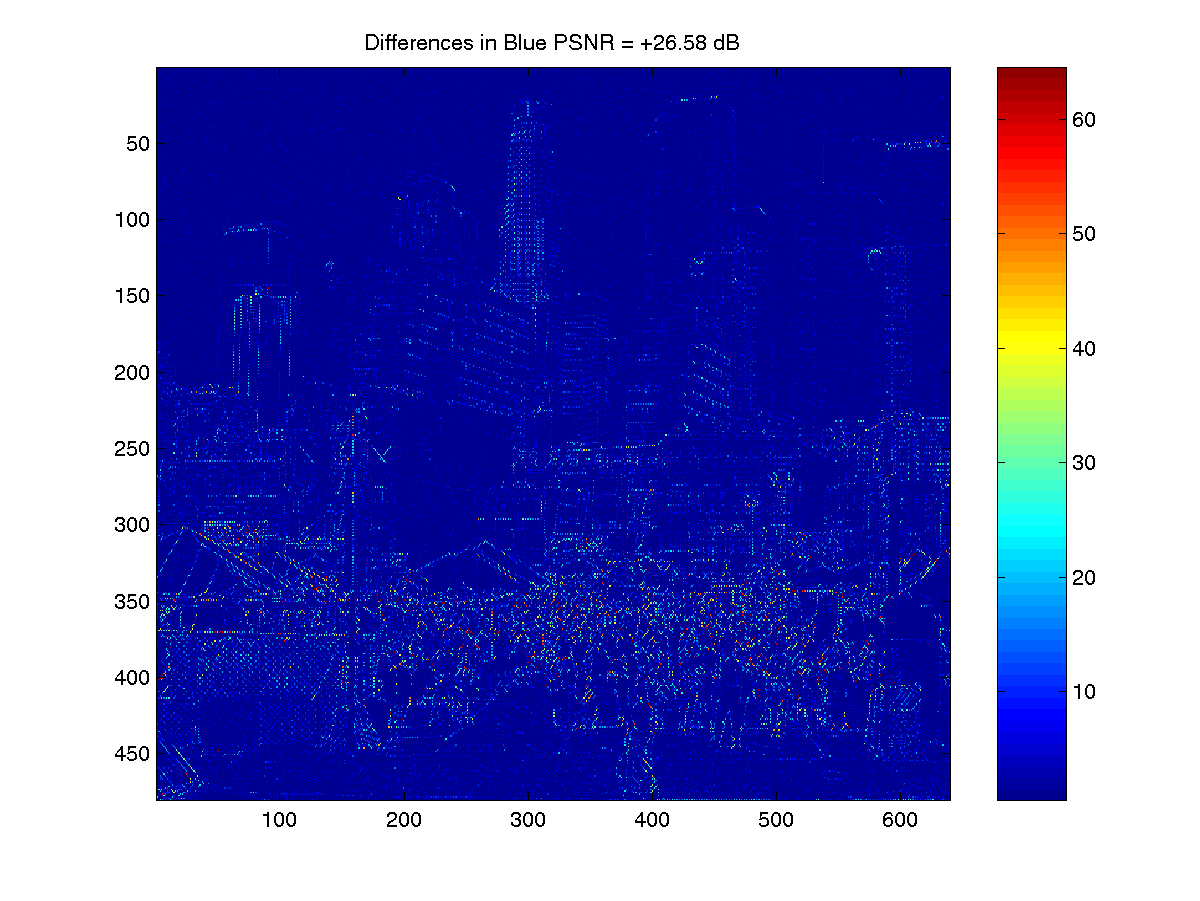
Difference b/t Original and Block Matched Interpolation (Blue)

PSNR of the above images vs. original

	Acharya & Tsai	MacMahon & matlab	MacMahon Noise Method
Red	26.4476	26.38	13.41
Green	31.8119	31.72	13.43
Blue	26.557	26.58	10.04

A noise generation algorithm was also run on the original image in the Bayer pattern and compared with the other two methods:

The noisy algorithm was indeed a success!

Summary

The PSNR's are not significantly in disagreement. The image was supplied by Acharya and Tsai. Speed was listed as one motivation in the original work…it took 1:30 to run in matlab! In any image processing problem special attention needs to be given to the edges, in email correspondence the authors stated that they did not recollect how the handled the edges. I used two calls to a custom padding/mirroring function to maintain the Bayer pattern and then extract the original 480 * 640 dimensions. This may account for the discrepancy in the PSNR.

Analyzing the image planes, the low-pass nature of the algorithm is notable. Most of the variance occurs in the lower half of the image.

If anyone wishes to examine my work for errors, I shall do so myself and report back to the original authors as they wished to be posted about any findings.

Thanks!

References:

Acharya, Tinku and Tsai, Ping-Sing. "A new block matching based color interpolation algorithm," IS&T/SPIE Conference on Color Imaging, San Jose, CA 1999.

Adams, James, Jr. "Interactions between color plane interpolation and other image processing functions in electronic photography," Electronic Imaging, Proc. SPIE, 2416, pp. 144-155, 1995.

Adams, James, Jr. "Design of practical color filter array interpolation algorithms for digital cameras," Proc. Of SPIE, vol. 3028, pp.117-125, 1997.

Adams et al., "Color Processing in Digital Cameras," Course Reader, 1999.

Freeman,W. "Median filter for reconstructing missing samples,", U.S.Patent #4,724,295 February 1988.