Because the Olympus camera automatically gamma-corrects the image for display, I need to undo this gamma-correction for the collected data to obtain the color information in linear space. Using the surface reflectance data for the Macbeth color checker gray series and their corresponding RGB values as reported by the camera, I wrote evalGamma.m to compute the gamma value by performing a least-squares fit to an exponential curve. To eliminate any offsets, I rescaled both sets of data to lie between 0 and 1 before computing the gamma value.
This is our data after normalization:
| Reflectance | 0.0000 | 0.0660 | 0.1962 | 0.3961 | 0.6560 | 1.0000 |
| RGB Average | 0.0000 | 0.2033 | 0.4168 | 0.6086 | 0.8038 | 1.0000 |
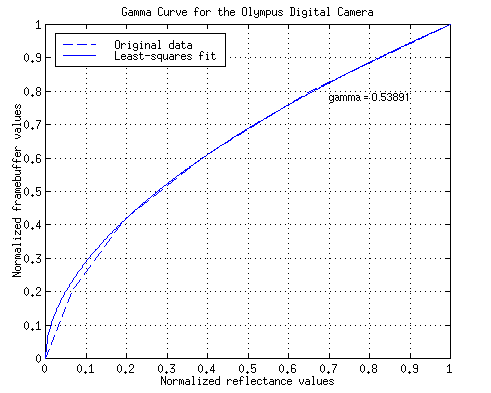
Here's a plot of the values above together with our analytic gamma curve. As you can see, our data agree very well with their least-squares exponential fit counterpart.

Figure 1: D-220L's gamma curve
The gamma value from these data is 0.5389. The reciprocal of that, which I will use to perform the inverse gamma-correction, is 1.8556. I wrote correctGamma.m to use this gamma information to transform any image into linear space.
Since we are interested only in the color of a pixel and not it's brightness, the fact that the camera automatically performs exposure compensation is really of no consequence. In most cases when I am comparing two sets of RGB values, I normalize them in such a way that they share the same value for one of the color components. When it is absolutely necessary to match the overall brightness between two images, I scale the R,G,B values of one image such that the average of (R+G+B) across all the pixels in one image is the same as that of the other image.
Another possible approach is to make their Y values equal. However, I avoided this approach because it scales each RGB component by a different factor. This may cause misleading hue shifts in the exposure-corrected image.