Implementation of the Ijspeert et al Modulation Transfer Functions

The modulation transfer function describes the optical quality of the eye by giving the amplitude response of the system to different spatial frequencies.  The blurring caused by the optics of the eye causes the amplitude to be reduced as spatial frequency increases.  Currently, one popular way to describe this transfer function is by using Westheimer's linespread function.  However, Westheimer's linespread function does not take into account certain differences between observers, like age and pupil size, that can cause the function to vary.

Using MTF data obtained by measuring overall and retinal contrast sensitivity functions, as well as straylight population data that provided more accurate information about the role of subject age and pigmentation, Ijspeert et al propose an improved description of the MTF and PSF.  This model fits the population data much more accurately than past models, and it functionally takes into account parameters for subject age, pupil size, and pigmentation.  A MATLAB implementation of this description is described below.

In order to calculate the MTF, PSF, and LSF curves, various constants that depend on the age, pupil size, and pigmentation parameters must first be computed.  The curves result from a linear combination of four terms--two relating to short-angle response and two to long-angle.  The width, or shape, of each term is described by b_i, and the corresponding weight given by c_i.

Dependence on Age

The dependence on age is addressed first.  From experimental straylight estimation, it has been found that terms corresponding to large-angle behavior increase with age relative to the short-angle terms.  This increase of long-angle scattering with age is represented by an age factor AF given by the MATLAB code:

D = 70;
AF = 1 + (age/D)^4;
 
D is a constant that represents the doubling age of long-angle scattering.  In addition, we compute a short-angle prefactor c_sa and a long-angle prefactor c_la that are employed later to help find expressions for the constants c_i:

c_sa = 1 / (1 + AF / (1/m - 1));
c_la = 1 / (1 + (1/m - 1) / AF);

Dependence on Pupil Size

Next, we take into account the pupil size.  We follow Ijspeert's assumption that pupil size only affects the short-angle terms.  The equations for the following three constants, obtained by data fitting, are first computed:

b = 9000 - 936*(AF^0.5);
d = 3.2;
e = (AF^0.5) / 2000;

Then, expressions for the short-angle terms c₁, c₂, b₁, and b₂ are computed:

c(1) = c_sa / (1 + (p/d)^2);
c(2) = c_sa / (1 + (d/p)^2);
beta(1) = (1 + (p/d)^2) / (b*p);  % in c/rad^(-1)
beta(2) = (1 + (d/p)^2) * (e - 1/(b*p)); % in c/rad^(-1)

Dependence on Pigmentation

The pigmentation state of the eye influences both isotropic and nonisotropic scattering.  The parameter m is chosen depending on the color of the eye; for example, m = 0.16 corresponds to the mean blue Caucasian eye, m = 0.106 corresponds to the mean brown Caucasian eye, and m = 0.056 the mean pigmented-skin dark-brown eye.  The Caucasian population mean is given by m = 0.142.  The large-angle terms c₃, c₄, b₃, and b₄ are now given by:

c(3) = c_la / ( (1 + 25*m) * (1 + 1/AF) );
c(4) = c_la - c(3);
beta(3) = (10 + 60*m - 5/AF)^(-1); % in c/rad^(-1)
beta(4) = 1;    % in c/rad^(-1)

Computing the PSF

With all constants found, the improved PSF function given by Ijspeert can be calculated as follows:

phi = 0.00005:0.000025:0.5;
sinphi2 = sin(phi).^2;
cosphi2 = cos(phi).^2;
beta2 = beta.^2;
for i = 1:4,
    f_beta(i, :) = beta(i) ./ ( 2*pi*( sinphi2 + beta2(i) * cosphi2 ).^(1.5) );
end
PSF = zeros(1, size(phi, 2));
for i = 1:4,
    PSF = PSF + c(i) * f_beta(i, :);
end

Notice the function f_beta varies from peaked to flat as b varies from small to 1, and that the derivative of f_beta is zero at zero angle.

Computing the LSF

f_beta has a simple LSF counterpart, given here by l_beta:

for i = 1:4,
    l_beta(i, :) = beta(i) ./ ( pi*( sinphi2 + beta2(i) * cosphi2 ));
end
LSF = zeros(1, size(phi, 2));
for i = 1:4,
    LSF = LSF + c(i) * l_beta(i, :);
end

Computing the MTF

Similarly, the MTF is computed by:

q = 0:0.1:50;
M_beta(:, :) = exp(-360*beta(:)*q);
MTF = zeros(1, size(q, 2));
for i = 1:4,
    MTF = MTF + c(i) * M_beta(i, :);
end

The complete MATLAB source code can be found here.

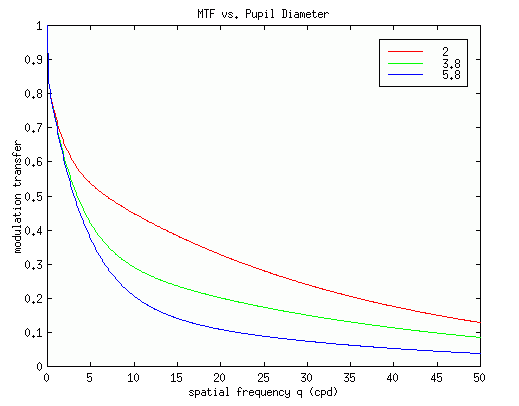
The following graph shows how much variation in MTF exists depending on the pupil diameter.  The MTF is significantly more depressed at larger pupil sizes.  Age is set to 35 years old, and the pigmentation parameter set to the Caucasian population mean of 0.142.

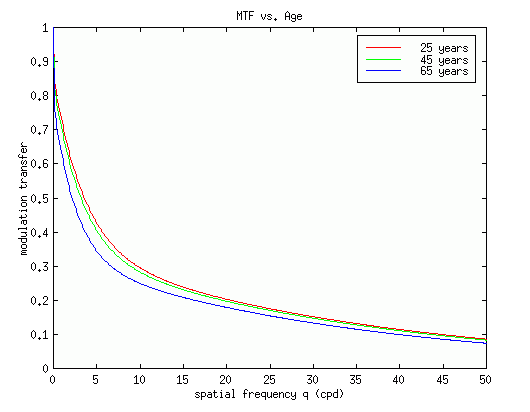
The following graph depicts how the MTF decreases with age, due to the increase of large-angle scattering with age.  The pupil diameter is held constant at 3.8 mm, and the Caucasian population mean of 0.142 is again used for the pigmentation parameter.

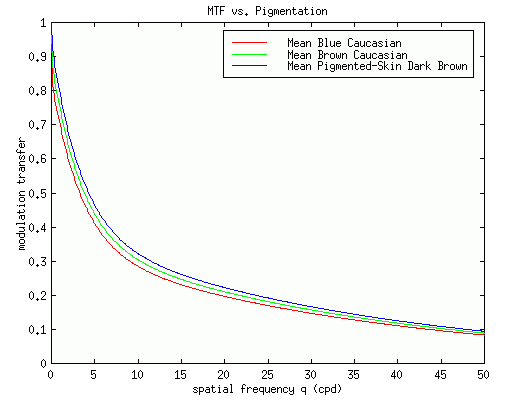
Variation of the MTF with the final parameter, pigmentation, is shown below.  There is a slightly higher response for darker pigments.  Age is set at 35 and pupil diameter at 3.8 mm.

Ijspeert, J. K., Van Den Berg, T., and Spekreijse, H.  1993.  A mathematical description of the foveal visual point spread function with parameters for age, pupil size and pigmentation.  Vision Res., 33:15-20.

Wandell, B. A.  1995.  Foundations of Vision.  Sinauer Associates, Sunderland, MA.